浙教版数学七年级上册期末冲刺满分攻略10 代数式及其运算求值（2）

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列说法正确的是（）

A、 $\frac{1}{x} + 1$ 是多项式 B、 $\frac{3 x + y}{3}$ 是单项式 C、 $- m n^{5}$ 是五次单项式 D、 $- x^{2} y - 2 x^{3} y$ 是四次多项式

查看试题解析
2. 下列说法错误是（）

A、数字2是单项式 B、单项式x的系数是1 C、 $x^{3} + x$ 是三次二项式 D、 $a^{2} b$ 与 $a b^{2}$ 是同类项

查看试题解析
3. 单项式 $\frac{π x y}{4}$ 的系数和次数分别是（）

A、 $\frac{1}{4}$ ， 1 B、 $\frac{1}{4}$ ， 2 C、 $\frac{π}{4}$ ， 1 D、 $\frac{π}{4}$ ， 2

查看试题解析
4. 下列各式： $- \frac{1}{5} a^{2} b^{2}$ ， $\frac{1}{2} x - 1$ ， $- 25$ ， $\frac{1}{x}$ ， $\frac{x - y}{2}$ ， $a^{2} - 2 a b$ ，其中单项式的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如果 $3 a^{m + 3} b^{4}$ 与 $a^{2} b^{n}$ 是同类项，则 $m n$ 的值为（）

A、4 B、-4 C、8 D、12

查看试题解析
6. 下列运算正确的是（）

A、 $2^{4} = 8$ B、 $2 x^{2} - x^{2} = 2$ C、 $2 a + 3 b = 5 a b$ D、 $2 x^{2} y - x^{2} y = x^{2} y$

查看试题解析
7. 下列各组单项式中是同类项的是（）

A、 $2 x$ 和 $2 y$ B、 $3 x^{2} y$ 和 $\frac{1}{2} x^{2} y$ C、 $m^{2} n$ 和 $m n^{2}$ D、3和 $3 x$

查看试题解析
8. 下列化简正确的是（）

A、8x-7y=x-y B、2a²b²-ab=ab C、9a²b-4ba²=5a²b D、5m-4m=1

查看试题解析
9. 张师傅以每件a元的价格购进了20件甲种商品，以每件b元的价格购进了30件乙种商品（a＞b）．根据市场行情，他将这两种商品都以 $\frac{a + b}{2}$ 元的价格出售．在这次买卖中，张师傅的盈亏状况为（　　）

A、赚了（25a+25b）元 B、亏了（20a+30b）元 C、赚了（5a-5b）元 D、亏了（5a-5b）元

查看试题解析
10. 如图，7张全等的小长方形纸片（既不重叠也无空隙）放置于矩形ABCD中，设小长方形的长为a ，宽为b（a＞b），若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（）

A、a B、b C、a+b D、a-b

查看试题解析

二、填空题

11. 合并同类项 $2 x - 7 y - 5 x + 11 y - 1 =$ .

查看试题解析
12. 若 $7 x^{m} y^{3}$ 和 $\frac{1}{2} y^{n} x^{2}$ 是同类项，则 $m - n =$ ．

查看试题解析
13. 若 $a^{2} - b^{2} - 4 - () = a^{2} + b^{2} + a b$ ，则括号内的式子为.

查看试题解析
14. 有按规律排列的一组单项式：x， $- \sqrt{2} x^{2}$ ， $\sqrt{3} x^{3}$ ， $- \sqrt{4} x^{4}$ ， $\sqrt{5} x^{5}$ ， …则第10个单项式是

查看试题解析
15. 对于任何有理数，我们规定符号 $\begin{array}{l} a & b \\ c & d \end{array}$ 的意义是 $\begin{array}{l} a & b \\ c & d \end{array} = a d - b c$ ，如 $\begin{array}{l} 1 & 2 \\ 3 & 4 \end{array} = 1 \times 4 - 2 \times 3 = - 2 .$ 当 $| x - 3 | + (y + 1)^{2} = 0$ 时， $\begin{array}{l} x^{2} - y & 2 \\ x^{2} & - 1 \end{array}$ 值为.

查看试题解析
16. 如图，将长为20cm、宽相等的长方形白纸，按如图所示的方法粘合起来，粘合部分的宽为2cm.则x张白纸粘合后的总长度为cm.

查看试题解析

三、计算题

17. 计算：

(1)、 $- 7 - (- 13) + (- 9)$

(2)、 $- 3^{2} \times {(- \frac{1}{3})}^{2} - (- 2)^{3} \div {(- \frac{1}{2})}^{2}$

(3)、 $(- \frac{5}{9} + \frac{1}{6} - \frac{7}{12}) \times (- 36)$

(4)、合并同类项： $4 a^{2} + 3 b^{2} + 2 a b - 4 a^{2} - 4 b^{2}$

查看试题解析
18. 数学家欧拉最先把关于x的多项式用记号f（x）来表示.例如：f（x）＝x²+x-1，当x＝a时.多项式的值用f（a）来表示，即f（a）＝a²+a-1.当x＝3时，f（3）＝3²+3-1＝11.

(1)、已知f（x）＝x²-2x+3，求f（1）的值.

(2)、已知f（x）＝mx²-2x-m，当f（-3）＝m-1时，求m的值.

(3)、已知f（x）＝kx²-ax-bk（a.b为常数），对于任意有理数k，总有f（-2）＝-2，求a，b的值.

查看试题解析
19. 在数学课上，老师给出了一道题目：“先化简再求值： $(x^{2} + □ x - 1) - 3 (\frac{1}{3} x^{2} - 2 x + 4)$ ，其中 $x = - 1$ ”， $□$ 中的数据被污染，无法解答，只记得 $□$ 中是一个实数，于是老师即兴出题，请同学们回答.

(1)、化简后的代数式中常数项是多少？

(2)、若点点同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果仍不变，求此时 $□$ 中数的值；

(3)、若圆圆同学把“ $x = - 1$ ”看成了“ $x = 1$ ”，化简求值的结果为-3，求当 $x = - 1$ 时，正确的代数式的值.

查看试题解析
20. 如图，两叠规格相同的杯子整齐地叠放在桌面上，请根据图中给出的数据信息，解答下列问题：

(1)、按如图所示叠放一起时，相邻两个杯子杯口之间的高度相差cm.

(2)、若x个杯子按如图所示整齐叠放在桌面上，求这些杯子的顶部距离桌面的距离（用含x的代数式表示）.当 $x = 10$ 时，求这些杯子的顶部距离桌面的距离.

查看试题解析
21. 放置在水平地面上两个无盖（朝上的面）的长方体纸盒，大小、形状如图.小长方体的长、宽、高分别为：a（cm）、b（cm）、c（cm）；大长方体的长、宽、高分别为： $1.5 a$ （cm）、 $2 b$ （cm）、 $2 c$ （cm）.

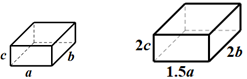(1)、做这两个纸盒共需要材料多少平分厘米？

(2)、做一个大的纸盒比做一个小的纸盒多多少平分厘米材料

查看试题解析
22. 一个两位数，它的十位数字是x，个位数字是y.若把十位数字与个位数字对调，得到一个新的两位数.请回答下列问题：

(1)、分别用含x，y的代数式表示这个两位数和对调后的新的两位数.

(2)、计算新数与原数的差.根据计算结果，你会得到哪些结论？写出你最认可的一条.

查看试题解析

23. 某市居民使用自来水按如下标准收费（水费按月缴纳）

居民月用水量

不超过 $10 m^{3}$ 的部分

超过 $10 m^{3}$ 但

不超过 $20 m^{3}$ 的部分

超过 $20 m^{3}$ 的部分

单价

2元 $/ m^{3}$

3元 $/ m^{3}$

4元 $/ m^{3}$

(1)、某用户一个月用了

16 m^{3}

水，求该用户这个月应缴纳的水费；

(2)、设某户月用水量为

n

立方米，当

n > 20

时，求该用户应缴纳的水费（用含

n

的代数式表示）；

(3)、甲、乙两用户一个月共用水

40 m^{3} .

已知甲用户缴纳的水费超过了20元，设甲用户用水

x m^{3}

，则甲、乙两用户一个月共缴纳水费多少元？（用含

x

的代数式表示）

查看试题解析

24. 七年级新学期，两摞规格相同准备发放的数学课本整齐地叠放在课桌面上，小英对其高度进行了测量，请根据图中所给出的数据信息，解答下列问题：

(1)、每本数学课本的厚度是cm；

(2)、若课本数x（本），请求出整齐叠放在桌面上的数学课本距离地面的高度的整式
（用x含的整式表示）；

(3)、现课桌面上有42本此规格的数学课本，整齐叠放成一摞，若从中取出15本，求余下的数学课本距离地面的高度．

查看试题解析