【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略16 图形的位似

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列说法正确的是（）．

A、相似图形一定是位似图形 B、位似图形不一定是相似图形 C、全等图形不可能是位似图形 D、位似图形一定是相似图形

查看试题解析
2. 下列图形中，不属于位似图形的是（）.

A、 B、 C、 D、

查看试题解析
3. 以原点 $O$ 为位似中心，作 $△ A B C$ 的位似图形 $△ A^{^{'}} B^{^{'}} C^{^{'}} ， △ A B C$ 与 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ 的位似比为3.若点 $C$ 的坐标为 $(4 ， 1)$ ，则点 $C^{^{'}}$ 的坐标为（）.

A、 $(12 ， 3)$ B、 $(- 12 ， 3)$ 或 $(12 ， - 3)$ C、 $(- 12 ， - 3)$ D、 $(12 ， 3)$ 或 $(- 12 ， - 3)$

查看试题解析
4. 用图形的位似把图形扩大或缩小时，下列说法中，正确的是（）.

A、位似中心要么取在图形的外部，要么取在图形的内部 B、位似中心取在图形的内部时，只能把图形缩小 C、当位似中心确定后，按要求放大或缩小的图形只能画一个 D、以上说法都不正确

查看试题解析
5. 如图，已知△ABC与△DEF是位似图形，O是位似中心，若OA＝2OD，则△ABC与△DEF的周长之比是（）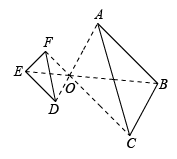

A、2：1 B、3：1 C、4：1 D、6：1

查看试题解析
6. 如图，四边形ABCD与四边形AEFG是位似图形，位似比为3∶2.若EF=6，则BC的长为（）

A、8 B、9 C、10 D、15

查看试题解析
7. 在平面直角坐标系中，已知点 $A (- 4 ， 2) ， B (- 6 ， - 4)$ ，以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把 $△ A B O$ 缩小，则点A的对应点 $A^{'}$ 的坐标是（）

A、 $(- 2 ， 1)$ B、 $(2 ， - 1)$ C、 $(- 8 ， 4)$ 或 $(8 ， - 4)$ D、 $(- 2 ， 1)$ 或 $(2 ， - 1)$

查看试题解析
8. 两个大小不一的五边形 $A B C D E$ 和五边形 $F B C H G$ 如图所示位置，点 $F$ 在线段 $A B$ 上，点 $H$ 在线段 $C D$ 上，对应连接并延长 $A F$ ， $E G$ ， $D H$ 刚好交于一点 $O$ ，则这两个五边形的关系是（）

A、一定相似 B、一定不相似 C、不一定相似 D、不能确定

查看试题解析
9. 如图，在直角坐标系中， $△ A B C$ 的三个顶点分别为 $A (1 ， 2) ， B (2 ， 1) ， C (3 ， 2)$ ，现以原点O为位似中心，在第一象限内作与 $△ A B C$ 的位似比为2的位似图形 $△ A^{'} B^{'} C^{'}$ ，则顶点 $C^{'}$ 的坐标是（）

A、 $(2 ， 4)$ B、 $(4 ， 2)$ C、 $(6 ， 4)$ D、 $(5 ， 4)$

查看试题解析
10. 如图，四边形 $A B C D$ 与四边形 $E F G H$ 位似，位似中心点是 $O$ ， $\frac{O E}{E A} = \frac{3}{4}$ ，则 $\frac{F G}{B C}$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中，O是 $B C$ 的中点，以点O为位似中心，作 $△ A B C$ 的位似图形 $△ D E F$ .若点A的对应点D是 $△ A B C$ 的重心，则 $△ A B C$ 与 $△ D E F$ 的位似比为.

查看试题解析
12. 在平面直角坐标系中，已知矩形OA₁B₁C₁与矩形OABC关于坐标原点O位似，且矩形OA₁B₁C₁的面积等于矩形OABC面积的4倍，若矩形OABC的顶点B的坐标为B（8，6），则B的对应点B₁的坐标为．

查看试题解析
13. 如图，△OAB与△OCD是以点O为位似中心的位似图形，位似比为1∶2，∠OCD=90°，CO=CD=2，则点B的坐标为．

查看试题解析
14.
如图，在直角坐标系中，△ABC的各顶点坐标为A（﹣1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为 $\frac{2}{3}$ ．则点A的对应点A′的坐标为

查看试题解析
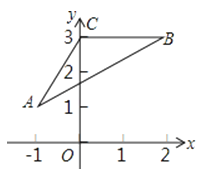15. 如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A、B、D在x轴上，若等边△BDE的边长为6，则点C的坐标为．

查看试题解析
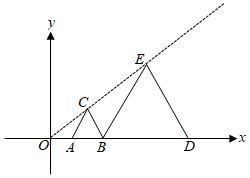16. 以下四个命题：①如果三角形一边的中点到其他两边距离相等，那么这个三角形一定是等腰三角形：②两条对角线互相垂直且相等的四边形是正方形：③一组数据2，4，6.4的方差是2；④△OAB与△OCD是以O为位似中心的位似图形，且位似比为1：4，已知∠OCD=90°，OC=CD．点A、C在第一象限．若点D坐标为（2 $\sqrt{3}$ ， 0），则点A坐标为（ $\frac{\sqrt{3}}{4}$ ， $\frac{\sqrt{3}}{4}$ ），其中正确命题有（填正确命题的序号即可）

查看试题解析

三、解答题

17.
如图，已知△DEO与△ABO是位似图形，△OEF与△OBC是位似图形．求证：OD•OC=OF•OA．

查看试题解析
18.
在放映电影时，我们需要把胶片上的图片放大到银幕上，以便人们欣赏．如图，点P为放映机的光源，△ABC是胶片上面的画面，△A′B′C′为银幕上看到的画面．若胶片上图片的规格是2.5cm×2.5cm，放映的银幕规格是2m×2m，光源P与胶片的距离是20cm，则银幕应距离光源P多远时，放映的图象正好布满整个银幕？

查看试题解析
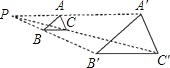19.
如图所示的平面图的比例尺是1：5000，根据图中所示的尺寸（单位：cm）．
（1）求围墙四边的实际长度；
（2）若墙上的四个小矩形全等，猜想四个小矩形是否是位似图形．

查看试题解析
20.
如图，△OAB以O为位似中心放大1倍到△A′OB′，写出变化前后各顶点的坐标，并指出坐标的变化规律．

查看试题解析
21.
如图，在平面直角坐标系中，△ABC和△A₁B₁C₁关于点E成中心对称，
（1）在图中标出点E，且点E的坐标为   ；
（2）点P（a，b）是△ABC边AB上一点，△ABC经过平移后点P的对应点P′的坐标为（a﹣6，b+2），请画出上述平移后的△A₂B₂C₂ ，此时A₂的坐标为     ， C₂的坐标为    ；
（3）若△A₁B₁C₁和△A₂B₂C₂关于点F成位似三角形，则点F的坐标为     ．

查看试题解析
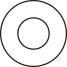
22.
如图，△ABC中，AD、BE是高．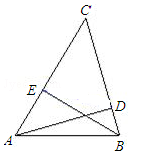

(1)、求证： $\frac{C D}{C E} = \frac{A C}{B C}$ ；

(2)、连接DE，那么△CDE与△CAB是位似图形吗？

查看试题解析
23.
如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，是的H，I，位于射线BC上，K位于射线BA上，而不需要求J必须位于AC上．这是他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC=12，在第（1）问的条件下，求长方形DEFG的面积．

查看试题解析