【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略15 相似多边形
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 下列与相似有关的命题中,正确的是( )
①所有的等腰三角形都相似;②所有的矩形都相似;③所有的正六边形都相似.
A、①②③ B、① C、② D、③2. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、3. 如图,用六个全等的直角三角形恰好拼成一大一小两个正六边形,则大正六边形与小正六边形的周长之比为( )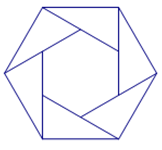 A、 B、 C、2 D、34. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A、 B、 C、2 D、34. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )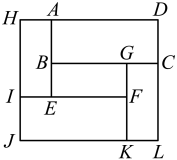 A、 B、 C、 D、5. 如图,在平行四边形中,点分别在边上, , 四边形四边形 , 相似比 , 则下列一定能求出面积的条件( )
A、 B、 C、 D、5. 如图,在平行四边形中,点分别在边上, , 四边形四边形 , 相似比 , 则下列一定能求出面积的条件( ) A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差6. 如图,矩形ABCD被分割成4个小矩形,其中矩形AEPH~矩形HDFP~矩形PEBG, , AC交HG,EF于点M,Q,若要求的而积,需知道下列哪两个图形的面积之差( )
A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差6. 如图,矩形ABCD被分割成4个小矩形,其中矩形AEPH~矩形HDFP~矩形PEBG, , AC交HG,EF于点M,Q,若要求的而积,需知道下列哪两个图形的面积之差( ) A、矩形AEPH和矩形PEBG B、矩形HDFP和矩形AEPH C、矩形HDFP和矩形PEBG D、矩形HDFP和矩形PGCF7. ABCD被分别平行于两边的四条线段EJ、FI、LG、KH分割成9个小平行四边形,面积分别为S1-9 , 已知ALME∽PICH∽ABCD.若知道S1-9中的n个,就一定能算出平行四边形ABCD的面积,则n的最小值是( ).
A、矩形AEPH和矩形PEBG B、矩形HDFP和矩形AEPH C、矩形HDFP和矩形PEBG D、矩形HDFP和矩形PGCF7. ABCD被分别平行于两边的四条线段EJ、FI、LG、KH分割成9个小平行四边形,面积分别为S1-9 , 已知ALME∽PICH∽ABCD.若知道S1-9中的n个,就一定能算出平行四边形ABCD的面积,则n的最小值是( ).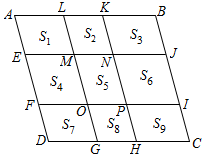 A、2 B、3 C、4 D、68. 将一张()纸片,以它的一边为边长剪去一个菱形,将余下的平行四边形中,再以它的一边为边长剪去一个菱形,若剪去两个菱形后所剩下的平行四边形与原来相似,则的相邻两边与的比值是( )A、 B、 C、或 D、或或9. 如图, , , , 是正方形边上的点,且 , 和将正方形剪切成四片进行重新拼接成四边形 , 若正方形和四边形的面积之比为 , 则( )
A、2 B、3 C、4 D、68. 将一张()纸片,以它的一边为边长剪去一个菱形,将余下的平行四边形中,再以它的一边为边长剪去一个菱形,若剪去两个菱形后所剩下的平行四边形与原来相似,则的相邻两边与的比值是( )A、 B、 C、或 D、或或9. 如图, , , , 是正方形边上的点,且 , 和将正方形剪切成四片进行重新拼接成四边形 , 若正方形和四边形的面积之比为 , 则( )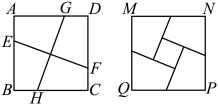 A、2 B、3 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、2 B、3 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )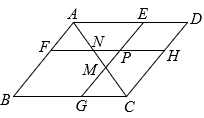 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若两个相似多边形的相似比是2:3,则它们的周长比是 .12. 两个相似多边形的周长之比为2:3,则它们的面积之比为.13. 如图,矩形ABCD中,AB=2,BC=4,剪去一个矩形ABEF后,余下的矩形EFDC∽矩形BCDA,则EC的长为.
 14. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.
14. 如图,把一个大长方形划分成三个全等的小长方形,若每一个小长方形均与大长方形相似,则的值为.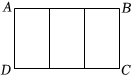 15. 如图所示,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 , 则的值为.
15. 如图所示,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 , 则的值为. 16. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
16. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .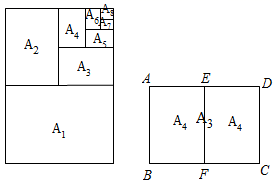
三、解答题
-
17. 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
 18. 如图,五边形ABCDEC∽五边形FGHIJ.求图中未知的边长x,y和∠H的大小
18. 如图,五边形ABCDEC∽五边形FGHIJ.求图中未知的边长x,y和∠H的大小 19. 如图,E,F分别是矩形ABCD一组对边AD,CB的中点.已知矩形AEFB∽矩形ABCD,求AB:BC的值.
19. 如图,E,F分别是矩形ABCD一组对边AD,CB的中点.已知矩形AEFB∽矩形ABCD,求AB:BC的值.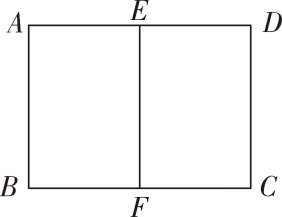 20.
20.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
 21. 如图,中,的平分线交于点 , 的平分线交于点.
21. 如图,中,的平分线交于点 , 的平分线交于点. (1)、求证:是菱形:(2)、若 , 则的值为.22. 几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN .
(1)、求证:是菱形:(2)、若 , 则的值为.22. 几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN .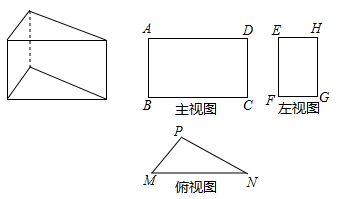 (1)、求BC及FG的长;(2)、若主视图与左视图两矩形相似,求AB的长;(3)、在(2)的情况下,求直三棱柱的表面积.23. 根据下列题目要求,解答下列问题:
(1)、求BC及FG的长;(2)、若主视图与左视图两矩形相似,求AB的长;(3)、在(2)的情况下,求直三棱柱的表面积.23. 根据下列题目要求,解答下列问题: (1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.
(1)、如图1,已知正方形ABCD和正方形BEFG,连接AG、CE.求证AG= CE.(2)、如图2,在矩形ABCD中,AB:BC=2:3,已知矩形ABCD∽矩形GBEF,相似比为AD:GF= , ∠ABG=30°,连接AG、CE,延长EF交BC于M.探究线段AG与CE的数量关系.(3)、如图3,已知矩形ABCD矩形GBEF,连接AG、CE、DF,发现线段AG、CE、DF存在这样的数量关系:AG2+CE2=DF2 , 请你对这个数量关系加以证明.