【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略14 相似三角形的应用
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 如图,线段AB,EF,CD分别表示人,竹竿,楼房的高度,且A,E,C在同一直线上.测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是( )
 A、25m B、26.5m C、50m D、51.5m2. 国旗法规定:所有国旗均为相似矩形,在下列四面国旗中,其中只有一面不符合标准,这面国旗是( )A、
A、25m B、26.5m C、50m D、51.5m2. 国旗法规定:所有国旗均为相似矩形,在下列四面国旗中,其中只有一面不符合标准,这面国旗是( )A、 B、
B、 C、
C、 D、
D、 3. 如图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏脚着地时捣头点E距离地面0.8米 ,则捣头点E着地时,踏脚点D距离地面( )
3. 如图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏脚着地时捣头点E距离地面0.8米 ,则捣头点E着地时,踏脚点D距离地面( )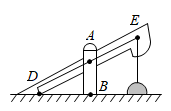 A、0.4 米 B、0.48米 C、0.5 米 D、0.8米4. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )
A、0.4 米 B、0.48米 C、0.5 米 D、0.8米4. 如图,树在路灯的照射下形成投影 , 若树离 , 树影 , 树与路灯的水平距离 , 则路灯的高度是( )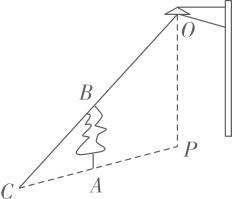 A、3 B、4 C、5 D、65. 如图,小李身高 , 在路灯O的照射下,影子不全落在地面上.小李离路灯的距离 , 落在地面上影长 , 留在墙上的影高 , 则路灯高为( )
A、3 B、4 C、5 D、65. 如图,小李身高 , 在路灯O的照射下,影子不全落在地面上.小李离路灯的距离 , 落在地面上影长 , 留在墙上的影高 , 则路灯高为( ) A、5m B、6m C、7.5m D、8m6. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 , 镜子 , 树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米
A、5m B、6m C、7.5m D、8m6. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 , 镜子 , 树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米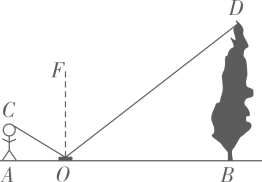 A、4 B、5 C、6 D、77. 如图1,是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面的宽度为( )
A、4 B、5 C、6 D、77. 如图1,是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面的宽度为( )
图1 图2
A、 B、 C、 D、8. 圆桌正上方的灯泡(看成一个点)发出的光线照射桌面后,在地面上形成阴影(如图).已知桌面的直径为1.2m.桌面距离地面0.9m,灯泡距离地面2.7m,则地面上阴影部分的面积为( ). A、0.36πm2 B、0.81πm2 C、2πm2 D、3.24πm29. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
A、0.36πm2 B、0.81πm2 C、2πm2 D、3.24πm29. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .
其中正确的结论有( )
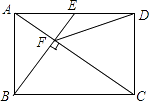 A、4个 B、3个 C、2个 D、1个10. 有一块锐角三角形余料 , 边的长为 , 边上的高为 , 现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A、4个 B、3个 C、2个 D、1个10. 有一块锐角三角形余料 , 边的长为 , 边上的高为 , 现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( ) A、5个 B、6个 C、7个 D、8个
A、5个 B、6个 C、7个 D、8个二、填空题
-
11. 为了测量河宽AB,有如下方法:如图,取一根标尺CD横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=15米,OC=10米,AC=20米,则河宽AB的长度为米.
 12. 如图,利用标杆DE测量楼高,点A、D、B在同一条直线上,DE⊥AC,BC⊥AC,垂足分别为E、C.若测得AE=1m,DE=1.5m,CE=5m,则楼高BC为m.
12. 如图,利用标杆DE测量楼高,点A、D、B在同一条直线上,DE⊥AC,BC⊥AC,垂足分别为E、C.若测得AE=1m,DE=1.5m,CE=5m,则楼高BC为m. 13. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.
13. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.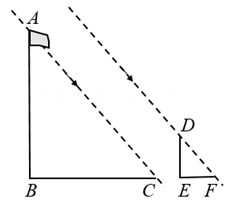 14. 如图,中边 , 高 , 正方形的四个顶点分别为三边上的点(点 , 为上的点,点为上的点,点为上的点),则正方形的边长为.
14. 如图,中边 , 高 , 正方形的四个顶点分别为三边上的点(点 , 为上的点,点为上的点,点为上的点),则正方形的边长为.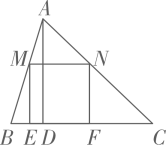 15. 如图,正方形的边在的边上,顶点D、G分别在边、上,如果 , 的面积是36,那么的长为 .
15. 如图,正方形的边在的边上,顶点D、G分别在边、上,如果 , 的面积是36,那么的长为 . 16. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地而上的点M在旋转中心O的正下方。某一时刻,太阳光线恰好垂直照射叶片 OA、OB ,此时各叶片影子在点M右侧成线段 CD ,测得MC=8.5m,CD=13m,垂直于地面的木棒 EF 与影子 FG 的比为2∶3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米.
16. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地而上的点M在旋转中心O的正下方。某一时刻,太阳光线恰好垂直照射叶片 OA、OB ,此时各叶片影子在点M右侧成线段 CD ,测得MC=8.5m,CD=13m,垂直于地面的木棒 EF 与影子 FG 的比为2∶3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米.
三、解答题
-
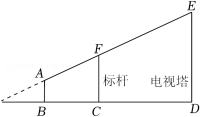
17. 如图所示,某测量工作人员头顶A与标杆顶点F、电视塔顶端E在同一直线上,已知此人眼睛距地面AB的长为1.6m , 标杆FC的长为3.2m , 且BC的长为2m , CD的长为5m , 求电视塔的高ED .
 18. 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连结AC并延长到点D,使CD= AC,连结BC并延长到点E,使CE= BC,连结DE.量得DE的长为15米,求池塘两端A,B的距离.
18. 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连结AC并延长到点D,使CD= AC,连结BC并延长到点E,使CE= BC,连结DE.量得DE的长为15米,求池塘两端A,B的距离. 19. 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
19. 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离. 20. 如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,求该古城墙CD的高度是多少m?
20. 如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,求该古城墙CD的高度是多少m? 21. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片 , , 此时各叶片影子在点M右侧成线段 , 测得 , , 设光线与地面夹角为α,测得
21. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片 , , 此时各叶片影子在点M右侧成线段 , 测得 , , 设光线与地面夹角为α,测得 (1)、求点O,M之间的距离.(2)、转动时,求叶片外端离地面的最大高度.22. 在中, , , , 点 , 分别是 , 线段上的点,且满足 , 连接 , 将绕着点逆时针旋转,记旋转角为 .
(1)、求点O,M之间的距离.(2)、转动时,求叶片外端离地面的最大高度.22. 在中, , , , 点 , 分别是 , 线段上的点,且满足 , 连接 , 将绕着点逆时针旋转,记旋转角为 . (1)、①当 , 时 ;
(1)、①当 , 时 ;②当时, .
(2)、如图 , 当时,过点作于点 , 过作于点 , 求出的值;(3)、当时,若为的中点,求在旋转过程中,线段长的最大值和最小值.23. 定义:按螺旋式分别延长n边形的n条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A1A2…An的边得A1′,A2′,…,An′,若多边形A1′A2′…An′与多边形A1A2…An相似,则多边形A1′A2′…An′就是A1A2…An的螺旋相似图形.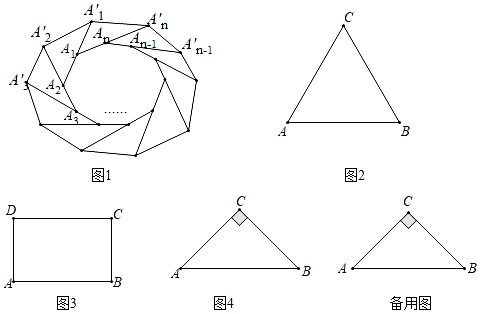 (1)、如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.(2)、如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.(3)、如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)
(1)、如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.(2)、如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.(3)、如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)