【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略13 相似三角形的性质与判定

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知△ABC的三条边长分别为3，5，6，若使△ABC∽△DEF，则△DEF的三条边长可以（）

A、4，6，7 B、4，7，8 C、12，10，8 D、18，15，9

查看试题解析
2. 如果两个相似三角形的周长之比为1：2，那么这两个三角形的面积之比为（）

A、1： $\sqrt{2}$ B、1：2 C、1：4 D、1：8

查看试题解析
3. 已知△ABC∽△A'B'C' ，BC=3，B'C'=1.8，则△ABC与△A'B'C'的相似比为（）．

A、2：3 B、3：2 C、5：3 D、3：5

查看试题解析
4. 下列命题正确的是（）．

A、所有的三角形都相似 B、所有的等腰三角形都相似 C、所有的等腰直角三角形都相似 D、所有的直角三角形都相似

查看试题解析
5. 如图，△ABC和△BCD是两个相似三角形，点D在AB上，∠BCD=∠A．若AD=6，BD=3，则BC的长是（）．

A、 $\sqrt{3}$ B、 $3 \sqrt{2}$ C、 $3 \sqrt{3}$ D、18

查看试题解析
6. 如图，在直角梯形 $A B C D$ 中， $∠ A B C = 90 °$ ， $A B = 8$ ， $A D = 3$ ， $B C = 4$ ，点 $P$ 为边 $A B$ 上一动点，若 $△ P A D$ 与 $△ P B C$ 是相似三角形，则满足条件的点 $P$ 的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，在平行四边形ABCD中E为AB的中点，F为AD上一点，EF与AC交于点H，FH＝3cm，EH＝6cm，AH＝4cm，则HC的长为（）

A、24cm B、22cm C、20cm D、18cm

查看试题解析
8. 如图，D，E分别是△ABC的边AB，BC上的点，且DE∥AC．若S_△_BDC：S_△_ADC＝1：3，则S_△_DOE：S_△_AOC的值为（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{9}$ D、 $\frac{1}{16}$

查看试题解析
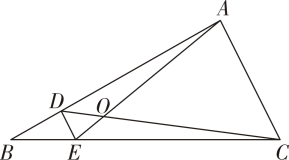9. 如图，在 $A B C$ 纸板中， $A C = 4$ ， $B C = 8$ ， $A B = 11$ ， $P$ 是 $B C$ 上一点，沿过点 $P$ 的直线剪下一个与 $△ A B C$ 相似的小三角形纸板．针对 $C P$ 的不同取值，三人的说法如下．下列判断正确的是（）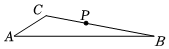

甲：若 $C P = 4$ ，则有 $3$ 种不同的剪法；

乙：若 $C P = 2$ ，则有 $4$ 种不同的剪法；

丙：若 $C P = 1$ ，则有 $3$ 种不同的剪法．

A、乙错，丙对 B、甲和乙都错 C、乙对，丙错 D、甲错，丙对

查看试题解析
10. 如图，直线 $y = k x + 7 k$ 与坐标轴相交于点A，B．分别以 $A B$ ， $O B$ 为直角边，以B为直角顶点，在 $△ A B O$ 的外部作等腰 $Rt △ A B C$ ，等腰 $Rt △ O B D$ ， $C D$ 与y轴相交于点E，则 $B E$ 的值为（）

A、4 B、7 C、 $\frac{7}{2}$ D、不能确定

查看试题解析

二、填空题

11. 如图，点P在△ABC的边AC上，请添加一个条件，使△ABP∽△ACB，

查看试题解析
12. 如图，在△ABC中，∠AED=∠B，若AB=10，AE=8，DE=6，则BC的长为.

查看试题解析
13. 如图，网高为0.8米，击球点到网的水平距离为3米，小明在打网球时，要使球恰好能打过网，且落点恰好在离网4米的位置上，则球拍击球的高度h为米.

查看试题解析
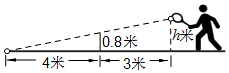14. 如图，点D是等边△ABC边AB上的一点，且AD：DB＝2：3，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF＝．

查看试题解析
15. 如图，若△ABC内一点P满足∠PAC＝∠PCB＝∠PBA，则称点P为△ABC的布罗卡尔点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现的，后来被数学爱好者、法国军官布罗卡尔重新发现，并用他的名字命名．布罗卡尔点的再次发现，引发了研究“三角形几何”的热潮．已知△ABC中，CA＝CB，∠ACB＝90°，点P为△ABC的布罗卡尔点．若PB＝4，则PA+PC＝．

查看试题解析
16. 如图，有一正方形ABCD，边长为 $2 \sqrt{2}$ ，点E是边CD上的中点，对角线BD上有一动点F，当顶点为A、B、F的三角形与顶点为D、E、F的三角形相似时，BF的值为．

查看试题解析

三、解答题

17. 如图，O是半圆的圆心，C、E是圆上的两点， $C D ⊥ A B$ ， $E F ⊥ A B$ ， $E G ⊥ C O$ .求证： $C D ＝ G F$ .

查看试题解析
18. 如图，在 $Δ A P B$ 中， $C$ ， $D$ 分别是 $A P$ ， $B P$ 上的点.且 $∠ C D P = ∠ A$ ， $A B = 8$ cm， $\frac{B P}{C P} = \frac{4}{3}$ ，求 $C D$ 的长.

查看试题解析
19. 如图，在矩形 $A B C D$ 中，点E，F分别在边 $A D$ ， $D C$ 上， $△ A B E ∽ △ D E F$ ， $D F > D E$ ， $A B = 9$ ， $A E = 12$ ， $D E = 3$ ，求 $F C$ 的长.

查看试题解析
20. 如图，AD、BC相交于点P，连结AC、BD，且∠1=∠2，AC=3，CP=2，DP=1，求BD的长.

查看试题解析
21. 如图，在Rt△ABC中，∠ABC＝90°，斜边AC的垂直平分线交BC于点D，交AC于点E，连接BE．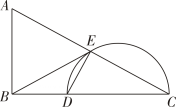

(1)、若BE是△AEC外接圆的切线，求∠C的大小；

(2)、当AB＝4，BC＝8时，求△DEC外接圆的半径．

查看试题解析
22. 从三角形 $($ 不是等腰三角形 $)$ 的一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中，一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

(1)、如图 $①$ ，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 °$ ，求证： $C D$ 为 $△ A B C$ 的完美分割线；

(2)、在 $△ A B C$ 中， $∠ A = 48 °$ ， $C D$ 是 $△ A B C$ 的完美分割线，且 $△ A C D$ 为等腰三角形，求 $∠ A C B$ 的度数；

(3)、如图 $②$ ，在 $△ A B C$ 中， $A C = 3$ ， $B C = \sqrt{3}$ ， $C D$ 是 $△ A B C$ 的完美分割线，且 $△ A C D$ 是以 $C D$ 为底边的等腰三角形，求完美分割线 $C D$ 的长．

查看试题解析
23. 正方形ABCD的边长为1，连接BD ，过点C作BD的平行线CE ， BE与CD相交于点F ，过点D作DH⊥BE ．

(1)、求△BDE的面积；

(2)、当∠CBE＝15°时，求BE的长；

(3)、若△EFC的面积记为S₁ ， △DFH的面积记为S₂ ， △DBF的面积记为S₃ ， △BFC的面积记为S₄ ， $\frac{C F}{C D} = k$ ，请用k的代数式表示 $\frac{S_{1} \cdot S_{2}}{S_{3} \cdot S_{4}}$ 的值．

查看试题解析