【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略12 平行线分线段成比例
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
 A、1 B、2 C、3 D、42. 如图,在中,点D,E分别在 , 上,且 , 下列式子不成立的是( )
A、1 B、2 C、3 D、42. 如图,在中,点D,E分别在 , 上,且 , 下列式子不成立的是( ) A、 B、 C、 D、3. 如图,已知 , 那么下列结论正确的是( )
A、 B、 C、 D、3. 如图,已知 , 那么下列结论正确的是( )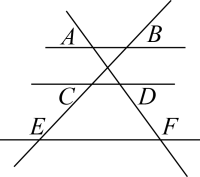 A、 B、 C、 D、4. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( )
A、 B、 C、 D、4. 如图,在中, , 边 , 上的中线 , 相交于点 , 若 , , 则( ) A、 B、 C、 D、5. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A、 B、 C、 D、5. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( ) A、 B、 C、6 D、6. 如图,是的外接圆,交于点E,垂足为点D,、的延长线交于点F.若 , , 则的长是( )
A、 B、 C、6 D、6. 如图,是的外接圆,交于点E,垂足为点D,、的延长线交于点F.若 , , 则的长是( ) A、19 B、20 C、21 D、227. 如图,在平行四边形ABCD中,E为的中点, , 在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( )
A、19 B、20 C、21 D、227. 如图,在平行四边形ABCD中,E为的中点, , 在现有点、线及字母的情况下,图中能表示的与面积相等的(除外)三角形有( ) A、3个 B、4个 C、5个 D、6个8. 如图,正方形中,分别在边上,相交于点G, 若 , 则 的值是( )
A、3个 B、4个 C、5个 D、6个8. 如图,正方形中,分别在边上,相交于点G, 若 , 则 的值是( ) A、 B、 C、 D、9. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A、 B、 C、 D、9. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )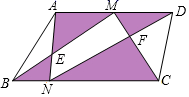 A、不变 B、一直变大 C、先减小后增大 D、先增大后减小10. 如图,P是▱ABCD内一点,连接P与▱ABCD各顶点,▱EFGH各顶点分别在边AP、BP、CP、DP上,且AE=2EP,EF∥AB.若△PEF与△PGH的面积和为1.则▱ABCD的面积为( )
A、不变 B、一直变大 C、先减小后增大 D、先增大后减小10. 如图,P是▱ABCD内一点,连接P与▱ABCD各顶点,▱EFGH各顶点分别在边AP、BP、CP、DP上,且AE=2EP,EF∥AB.若△PEF与△PGH的面积和为1.则▱ABCD的面积为( ) A、4 B、6 C、12 D、18
A、4 B、6 C、12 D、18二、填空题
-
11. 如图,在中, , , , , 则的长为 .
 12. 如图,在△ABC中,D,E两点分别在AB,AC边上,DE∥BC.如果 ,AC=10,那么EC=.
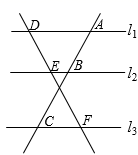
12. 如图,在△ABC中,D,E两点分别在AB,AC边上,DE∥BC.如果 ,AC=10,那么EC=. 13. 如图,直线 , 直线交 , , 于点A,C,E,直线交 , , 于点B,D,F.若 , , 则的长为.
13. 如图,直线 , 直线交 , , 于点A,C,E,直线交 , , 于点B,D,F.若 , , 则的长为. 14. 如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,则FN:ND= .
14. 如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,则FN:ND= . 15. 矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则BF=.
15. 矩形ABCD中,AB=5,BC=4,点E是AB边上一点,AE=3,连接DE,点F是BC延长线上一点,连接AF,且∠F=∠EDC,则BF=. 16. 如图,在▱ABCD中,以AB为直径的⊙O与BC边的中点交于点E,与对角线AC交于点F,作EG⊥AC,垂足为M.若FA=3CF,则的值为.
16. 如图,在▱ABCD中,以AB为直径的⊙O与BC边的中点交于点E,与对角线AC交于点F,作EG⊥AC,垂足为M.若FA=3CF,则的值为.
三、解答题
-
17. 如图,直线l1∥l2∥l3 , 若AB=6,BC=10,EF=9,求DE的长.
 18.
18.已知,如图,点A,B,C分别在△EFD的各边上,且AB∥DE,BC∥EF,CA∥FD,求证:A,B,C分别是△EFD各边的中点.
 19. 如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.
19. 如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长. 20. 对于平行线,我们有这样的结论:如图1,AB∥CD,AD,BC交于点O,则= .
20. 对于平行线,我们有这样的结论:如图1,AB∥CD,AD,BC交于点O,则= .请利用该结论解答下面的问题:
如图2,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
 21. )如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
21. )如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.(1)DQ=10米时,求△APQ的面积.
(2)当DQ的长为多少米时,△APQ的面积为1600平方米.
 22. 定义:如图1,点、把线段分割成三条线段、和 , 若 , 则称是线段的比例中段,、是线段的中段分点.
22. 定义:如图1,点、把线段分割成三条线段、和 , 若 , 则称是线段的比例中段,、是线段的中段分点. (1)、已知点、是线段的中段分点.
(1)、已知点、是线段的中段分点.①若 , , 则 ▲ ;
②在图1中,若 , , 求的长.
(2)、如图2,在中,是线段的比例中段,、分别是线段、延长线上的点,且 , 、的延长线分别交线段于点 , .探究是否为线段的比例中段,如果是,请给出证明,如果不是,请说明理由..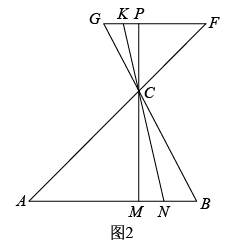 23. 【问题提出】如图1, 中,线段 的端点 分别在边 和 上,若位于 上方的两条线段 和 之积等于 下方的两条线段 和 之积,即 ,则称 是 的“友好分割”线段.
23. 【问题提出】如图1, 中,线段 的端点 分别在边 和 上,若位于 上方的两条线段 和 之积等于 下方的两条线段 和 之积,即 ,则称 是 的“友好分割”线段. (1)、如图1,若 是 的“友好分割”线段,
(1)、如图1,若 是 的“友好分割”线段, ,求 的长; (2)、【发现证明】如图2, 中,点F在 边上, 交 于D, 交 于E,连结 ,求证: 是 的“友好分割”线段;(3)、【综合运用】如图3, 是 的“友好分割”线段,连结 并延长交 的延长线于F,过点A 画 交 的外接圆于点G,连结 ,设 .
,求 的长; (2)、【发现证明】如图2, 中,点F在 边上, 交 于D, 交 于E,连结 ,求证: 是 的“友好分割”线段;(3)、【综合运用】如图3, 是 的“友好分割”线段,连结 并延长交 的延长线于F,过点A 画 交 的外接圆于点G,连结 ,设 .①求y关于x的函数表达式;
②连结 ,当 时,求 的值.