【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略11 比例线段
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 已知x:y=5:2,则下列各式不正确的是( )A、 B、 C、 D、2. 已知3a=2b(a≠0,b≠0),下列变形正确的是( )A、 B、 C、 D、3. 下列四条线段中,不能成比例的是( )A、a=2,b=3,c=4,d=6 B、a=1,b= , c= , d= C、a=4,b=5,c=6,d=10 D、a=1,b=2,c= , d=24. 已知 , 则的值为( ).A、 B、 C、-5 D、55. 在相同时刻的物高与影长成比例,小明的身高为.某一时刻他在地面上的影长为 , 同一时刻位于该处的一座古塔在地面上的影长为 , 则古塔的高为( ).A、 B、 C、 D、6. 如图所示,已知是线段AB的黄金分割点 , 则下列结论中,正确的是( ).
 A、 B、 C、 D、7. 在一幅比例尺为1:1000000的地图上,量得某座大桥长5.5厘米,这座大桥的实际长度是( )A、55米 B、10千米 C、55千米8. 已知a,b,c为非零实数,且满足 , 则一次函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列命题中,正确的是( )A、相似三角形的角平分线的比等于相似比 B、所有的菱形都相似 C、一般来说,一条线段的黄金分割点有两个 D、如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、 B、 C、 D、7. 在一幅比例尺为1:1000000的地图上,量得某座大桥长5.5厘米,这座大桥的实际长度是( )A、55米 B、10千米 C、55千米8. 已知a,b,c为非零实数,且满足 , 则一次函数的图象一定经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 下列命题中,正确的是( )A、相似三角形的角平分线的比等于相似比 B、所有的菱形都相似 C、一般来说,一条线段的黄金分割点有两个 D、如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )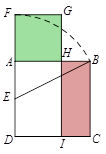 A、
A、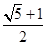 B、
B、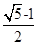 C、
D、1
C、
D、1
二、填空题
-
11. 已知 , 则的值为 .12. 一张浙江省地图的比例尺为1:4000000,杭州到嘉兴的图上距离约是2cm,则杭州到嘉兴的实际距离约为13. 如图,在中, , 分别是和上的点, , , , 且 , 则 .
 14. 已知线段a=2,b=8,则a,b的比例中项线段长是 .15. 已知点C为线段AB的黄金分割点(AC>BC),已知AB=2,则AC= .16. 在芯片制作过程中, 需要对 的矩形区域进行划区处理, 划成如图所示的“ ” 的形式, 其中 为竖式矩形 为横式矩形 , 则芯片被利用区域的长 的值为 cm .
14. 已知线段a=2,b=8,则a,b的比例中项线段长是 .15. 已知点C为线段AB的黄金分割点(AC>BC),已知AB=2,则AC= .16. 在芯片制作过程中, 需要对 的矩形区域进行划区处理, 划成如图所示的“ ” 的形式, 其中 为竖式矩形 为横式矩形 , 则芯片被利用区域的长 的值为 cm .

三、解答题
-
17. 已知线段c是线段a,b的比例中项,若 , ,求线段c的长.18. 已知,在△ABC中,AB=c,BC=a,AC=b, ,求△ABC的面积.19.
小知识:古希腊的毕达哥拉斯,在2500年前曾经大胆断言,一条线段(AB)的某一部分(AC)与另一部分(BC)之比,如果正好等于另一部分(BC)同整个线段(AB)的比(即BC2=AC.AB),那么这样的比例会给人一种美感,后来我们将分割这条线段(AB)的点C称为线段AB的“黄金分割点”,
在主持节目时,主持人站在舞台的黄金分割点处最自然得体,那么在长20米的舞台AB上,主持人从A点到B点走多少米,他的站台最得体?(取=1.4,=1.7,=2.2)
 20. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
20. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少? 21. 我们把长与宽之比为的矩形纸片称为标准纸.如图,将一张标准纸ABCD(AB<BC)对折,得到矩形纸片EFGH.判断图中两个矩形的长与宽是否成比例,并说明理由.
21. 我们把长与宽之比为的矩形纸片称为标准纸.如图,将一张标准纸ABCD(AB<BC)对折,得到矩形纸片EFGH.判断图中两个矩形的长与宽是否成比例,并说明理由. 22. 在比例尺为1:10000的地图上,有甲、乙两个相似三角形区域,其周长分别为10cm和15cm.(1)、求它们的面积比;(2)、若在地图上量得甲的面积为16cm2 , 则乙所表示的实际区域的面积是多少平方米?23. 如图甲所示,C将线段AB分成两部分,如果 , 那么称为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分测线”.现给出“黄金分割线”的定义:直线将一个面积为的图形分成两部分,这两部分的面积分别为 , 如果 , 那么称直线为该图形的“黄金分割线”.请回答下列问题:
22. 在比例尺为1:10000的地图上,有甲、乙两个相似三角形区域,其周长分别为10cm和15cm.(1)、求它们的面积比;(2)、若在地图上量得甲的面积为16cm2 , 则乙所表示的实际区域的面积是多少平方米?23. 如图甲所示,C将线段AB分成两部分,如果 , 那么称为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分测线”.现给出“黄金分割线”的定义:直线将一个面积为的图形分成两部分,这两部分的面积分别为 , 如果 , 那么称直线为该图形的“黄金分割线”.请回答下列问题: (1)、研究小组猜想:在中,若为AB边的黄金分割点(如图乙所示),则直线CD是的“黄金分割线”.你认为这种猜想对吗?为什么?(2)、三角形的中线是否也是该三角形的“黄金分割线”?请说明理由.(3)、研究小组在进一步探究中发现:过点任作一条直线交AB于点 , 再过点作直线 , 交AC于点 , 连结EF(如图丙所示),则直线EF也是的“黄金分割线”.请说明理由.
(1)、研究小组猜想:在中,若为AB边的黄金分割点(如图乙所示),则直线CD是的“黄金分割线”.你认为这种猜想对吗?为什么?(2)、三角形的中线是否也是该三角形的“黄金分割线”?请说明理由.(3)、研究小组在进一步探究中发现:过点任作一条直线交AB于点 , 再过点作直线 , 交AC于点 , 连结EF(如图丙所示),则直线EF也是的“黄金分割线”.请说明理由.