人教版(吉林地区)初中数学2023-2024学年九年级上学期期末模拟卷(一)
试卷更新日期:2023-12-12 类型:期末考试
一、选择题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )A、13 B、5 C、 D、3. 如图,在△ABC纸片中,∠CAB=75°,将其绕点A逆时针旋转到△AB'C的位置,连接CC,CC'∥AB,则旋转的最小角度为( )
2. 已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )A、13 B、5 C、 D、3. 如图,在△ABC纸片中,∠CAB=75°,将其绕点A逆时针旋转到△AB'C的位置,连接CC,CC'∥AB,则旋转的最小角度为( ) A、30° B、35° C、40° D、50°4. 暗箱中有大小质量都相同的红色,黑色小球若干个,随机摸出红球的概率是 , 已知黑色小球有个,则红球的数量为( )A、 B、 C、 D、5. 要组织一次篮球邀请赛,参赛的每两个队之间都要赛一场,赛程计划安排7天,每天安排4场比赛.如果共有x个队参赛,为了求出x , 根据题意可列方程( )A、x(x+1)=4×7 B、x(x-1)=4×7 C、 D、6. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A、30° B、35° C、40° D、50°4. 暗箱中有大小质量都相同的红色,黑色小球若干个,随机摸出红球的概率是 , 已知黑色小球有个,则红球的数量为( )A、 B、 C、 D、5. 要组织一次篮球邀请赛,参赛的每两个队之间都要赛一场,赛程计划安排7天,每天安排4场比赛.如果共有x个队参赛,为了求出x , 根据题意可列方程( )A、x(x+1)=4×7 B、x(x-1)=4×7 C、 D、6. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )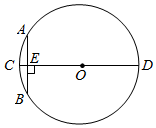 A、12寸 B、24寸 C、13寸 D、26寸7. 已知二次函数在时,函数有最大值1,则a的值是( )A、 B、 C、或 D、或8. 抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),直线y=kx+m经过点(-1,0),直线y=kx+m与抛物线y=ax2+bx+c另一个交点的横坐标是4,它们的图象如图所示,有以下结论:
A、12寸 B、24寸 C、13寸 D、26寸7. 已知二次函数在时,函数有最大值1,则a的值是( )A、 B、 C、或 D、或8. 抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),直线y=kx+m经过点(-1,0),直线y=kx+m与抛物线y=ax2+bx+c另一个交点的横坐标是4,它们的图象如图所示,有以下结论:①抛物线对称轴是直线x=1;②a-b+c=0;③-1<x<3时,ax2+bx+c<0;④若a= , 则k= .
其中正确的个数为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 已知关于x方程有一个根为-1,则方程的另一个根为 .10. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,如果水面下降1m,那么水面宽度增加m.
 11. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转,得到△EDC,使点B的对应点D恰好落在AB边上,AC、ED交于点F.若∠BCD=50°,则∠EFC=度.
11. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转,得到△EDC,使点B的对应点D恰好落在AB边上,AC、ED交于点F.若∠BCD=50°,则∠EFC=度. 12. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 .
12. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 . 13. 兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m ,高度CD为 m.
13. 兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m ,高度CD为 m.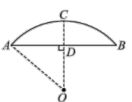 14. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
14. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=60°;②∠CED= ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是 .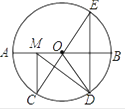
三、计算题
-
15. 解方程:(1)、(配方法);(2)、 .
四、解答题
-
16. 如图,在平面直角坐标系中,已知点 , , .
 (1)、画出关于原点O成中心对称的 , 并写出点B的对应点的坐标;(2)、画出将绕点逆时针旋转90°后得到的 .17. 小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.(1)、请用画树形图或列表的方法求小敏去看比赛的概率;(2)、哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.18. 已知二次函数y=(x-m)2-(x -m).(1)、试说明该二次函数的图象与x轴必有两个交点.(2)、若该二次函数图象的顶点坐标为( , n),求m,n的值.19. 周末,小明和小红约着一起去公园跑步锻炼身体若两人同时从地出发,匀速跑向距离处的地,小明的跑步速度是小红跑步速度的倍,那么小明比小红早分钟到达地.(1)、求小明、小红的跑步速度;(2)、若从地到达地后,小明以跑步形式继续前进到地整个过程不休息 , 据了解,在他从跑步开始前分钟内,平均每分钟消耗热量卡路里,超过分钟后,每多跑步分钟,平均每分钟消耗的热量就增加卡路里,在整个锻炼过程中,小明共消耗卡路里的热量,小明从地到地锻炼共用多少分钟.20. 如图,在△ABC中,∠B=20°,∠ACB= =30°,AB=2 cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)、画出关于原点O成中心对称的 , 并写出点B的对应点的坐标;(2)、画出将绕点逆时针旋转90°后得到的 .17. 小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将两人抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.(1)、请用画树形图或列表的方法求小敏去看比赛的概率;(2)、哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.18. 已知二次函数y=(x-m)2-(x -m).(1)、试说明该二次函数的图象与x轴必有两个交点.(2)、若该二次函数图象的顶点坐标为( , n),求m,n的值.19. 周末,小明和小红约着一起去公园跑步锻炼身体若两人同时从地出发,匀速跑向距离处的地,小明的跑步速度是小红跑步速度的倍,那么小明比小红早分钟到达地.(1)、求小明、小红的跑步速度;(2)、若从地到达地后,小明以跑步形式继续前进到地整个过程不休息 , 据了解,在他从跑步开始前分钟内,平均每分钟消耗热量卡路里,超过分钟后,每多跑步分钟,平均每分钟消耗的热量就增加卡路里,在整个锻炼过程中,小明共消耗卡路里的热量,小明从地到地锻炼共用多少分钟.20. 如图,在△ABC中,∠B=20°,∠ACB= =30°,AB=2 cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.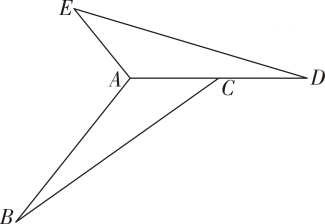 (1)、指出旋转中心,并求出旋转的度数;(2)、求出∠BAE的度数和AE的长.21. 如图所示,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)、指出旋转中心,并求出旋转的度数;(2)、求出∠BAE的度数和AE的长.21. 如图所示,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM. (1)、证明:△DEF≌△DMF.(2)、若 , 求FM的长.22. 如图,四边形内接于 , 连接 , , .
(1)、证明:△DEF≌△DMF.(2)、若 , 求FM的长.22. 如图,四边形内接于 , 连接 , , .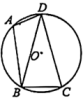 (1)、求的大小;(2)、若的半径为3,求的长.
(1)、求的大小;(2)、若的半径为3,求的长.五、实践探究题
-
23. 阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如图1∠ABC所示.同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图2)
证明:∵AB切⊙O于点A,∴∠CAB=90°,又∵AC是直径,∴∠P=90°∴∠CAB=∠P

问题拓展:若AC不经过圆心O(如图3),该结论:弦切角∠CAB=∠P还成立吗?请说明理由.
知识运用:如图4,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC.
24. 【创新是民族进步的灵魂华为一直在科技领域追求极致美学、极致工艺、极致创新真正意义上做到遥遥领先】我们不妨约定:若 , 是关于的函数,当时,总有 , 并存在满足 , 使得 , 我们则称函数对在领域“阶领先”.(1)、已知一次函数对在领域“阶领先”,求的值;(2)、已知二次函数为常数的图象与一次函数相交于 , 两点,其横坐标分别记为和 , 且满足 , 请判断二次函数对一次函数能否在领域“阶领先”,请说明理由;(3)、已知二次函数的顶点经过一次函数的图象,若二次函数对一次函数在领域“阶领先”,求二次函数的解析式.
-