人教版（吉林地区）初中数学2023-2024学年八年级上学期期末模拟卷（二）

试卷更新日期：2023-12-12 类型：期末考试

进入出卷网下载

一、选择题

1. 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 平面直角坐标系中的点A（-3，2）关于x轴对称的点的坐标是（　　）

A、（3，-2） B、（3，2） C、（-3，2） D、（-3，-2）

查看试题解析
3. 如图，小明从边长为 $a$ 的正方形纸片中剪去边长为 $b$ 的小正方形纸片，则图中阴影部分的面积为（）

A、 ${(a + b)}^{2}$ B、 ${(a - b)}^{2}$ C、 $(a + b) (a - b)$ D、 $(a + 2 b) (a - 2 b)$

查看试题解析
4. 下列计算中，正确的是（）

A、 $a^{4} \cdot a^{2} = a^{8}$ B、 ${(a b)}^{3} = a^{3} b$ C、 ${(a^{5})}^{2} = a^{7}$ D、 $a^{6} \div a^{2} = a^{4}$

查看试题解析
5. 若关于x的分式方程 $\frac{6}{x - 1} = \frac{x + 3}{x (x - 1)} - \frac{k}{x}$ 无解，则k的取值是（）

A、 $k = - 3$ B、 $k = - 3$ 或 $k = - 5$ C、 $k = 1$ D、 $k = 1$ 或 $k = - 5$

查看试题解析

6. 下面是马小虎的答卷，他的得分应是（）

姓名马小虎得分？

判断题（每小题20分，共100分）

（1）代数式 $\frac{6}{x}$ ， $\frac{m + n}{m - n}$ 是分式．（√）（2）当x＝-1时，分式 $\frac{x}{x + 1}$ 无意义．（×）

（3） $\frac{a^{2} + b^{2}}{a + b}$ 不是最简分式．（×）（4）若分式 $\frac{| x | - 2}{x + 2}$ 的值为0，则x的值为±2．（√）

（5）分式 $\frac{y^{2}}{x + y}$ 中x ， y的值均扩大为原来的2倍，分式的值保持不变．（×）

A、40分 B、60分 C、80分 D、100分

查看试题解析

7. 如图，在△ABC中，∠ABC ， ∠ACB的平分线BE，CD相交于点F ， ∠ABC＝52°，∠A=60°则∠BFC＝（　　）

A、128° B、120° C、119° D、121°

查看试题解析
8. 如图，在 $△ A O B$ 和 $△ C O D$ 中， $O A = O B ， O C = O D ， O A < O C ， ∠ A O B = ∠ C O D = 36 °$ ．连接AC，BD交于点M，连接OM．则下列结论：① $∠ A M B = 36 °$ ；② $A C = B D$ ；③ $O M$ 平分 $∠ A O D$ ；④ $M O$ 平分 $∠ A M D$ ．其中正确结论的个数为（　　）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

9. $x^{m} = 2 ， x^{n} = 3 ，$ ， $x^{4 m - 2 n} =$ ．

查看试题解析
10. 甲、乙两人同时从学校出发，去距离学校15千米的农场参加劳动．甲的速度是乙的1.2倍，结果甲比乙早到10分钟，求甲和乙的速度各是多少？设乙的速度为 $x$ 千米/小时，则根据题意可列方程为．

查看试题解析
11. 已知两根长度分别为3cm.7cm的木伟，若想钉一个等腰下角形木架，第三根木棒的长度应该是 cm．

查看试题解析
12. 如图，△ABC中，BC的垂直平分线l与AC相交于点D，若△ABD的周长为12cm，
则AB+AC=cm．

查看试题解析
13. 如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2＝度．

查看试题解析
14. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E ， S_△_ABC＝24，DE＝4，AB＝5，则AC的长是．

查看试题解析

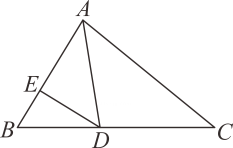
三、计算题

15. 因式分解：

(1)、 $2 x^{2} y - 8 x y + 8 y$

(2)、 ${(m^{2} - 5)}^{2} + 2 (m^{2} - 5) + 1$

查看试题解析
16. 先化简，再求值： $(x - \frac{3 x}{x + 1}) \div \frac{x - 2}{x^{2} + 2 x + 1}$ ，其中 $x$ 满足 $x^{2} + x - 2023 = 0$

查看试题解析

四、作图题

17. 如图，已知△ABC.

(1)、画AB边上的中线CD；

(2)、画BC边上的高线AE；

(3)、用尺规作△ABC的角平分线BF（保留痕迹，不写作法）.

查看试题解析
18. 如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个顶点的坐标分别为A（-4，1），B（-3，3），C（-1，2）．画出△ABC关于x轴对称的△A₁B₁C₁ ，点A、B、C的对称点分别是点A₁、B₁ ， C₁ ，直接写出点A₁ ， B₁、C₁的坐标：A₁（ ▲ ， ▲ ），B₁ ▲ ， ▲ ），C₁（ ▲ ， ▲ ）．

查看试题解析

五、解答题

19. 已知 $a - b = 7$ ， $a b = - 12$ ．

(1)、求 $a^{2} + b^{2}$ 的值；

(2)、求 $a + b$ 的值．

查看试题解析
20. 已知： $a > 0$ ， $b > 0$ ， $\frac{a}{b} + \frac{b}{a} + 2 = a b$ ，且 $a \neq b$ .

(1)、求证： $a + b = a b$ ；

(2)、求 $\frac{a^{2}}{2 a - 2 b} - \frac{a^{2}}{2 a + 2 b} - \frac{a b^{2} + a^{2} b}{2 a^{2} - 2 b^{2}}$ 的值.

查看试题解析
21. “一年好景君须记，最是雪峰橘黄时”.10月20日“香满雪峰桔约洞口———2023年湖南洞口雪峰蜜桔文化节”盛大开幕，吸引了全国各地商人纷至沓来．已知甲到洞口距离为200千米，乙到洞口的距离为180千米．甲、乙两人同时开车去洞口，甲开车比乙开车的速度快10千米/小时，结果两辆车同时到达．求乙的车速．

查看试题解析
22. 如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．

查看试题解析

六、实践探究题

23. 阅读理解以下材料内容：
完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题．
例：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a + b = 3$ ， $a b = 1$ ，
      $∴ (a + b)^{2} = 9$ ， $2 a b = 2$ ．
      $∴ (a + b)^{2} = a^{2} + 2 a b + b^{2}$ ．
      $∴ a^{2} + b^{2} = 7$ ．
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 4$ ， $x^{2} + y^{2} = 10$ ，求 $x y$ 的值；应用以上知识进行思维拓展；

(2)、如图，点 $C$ 是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向两边作正方形，若 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积．

查看试题解析
24. 综合与实践
数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．

(1)、发现问题：如图1，在 $△ A B C$ 和 $△ A E F$ 中， $A B = A C$ ， $A E = A F$ ， $∠ B A C = ∠ E A F = 30 °$ ，连接 $B E$ ， $C F$ ，延长 $B E$ 交 $C F$ 于点 $D$ ．则 $B E$ 与 $C F$ 的数量关系：， $∠ B D C =$ $°$ ；

(2)、类比探究：如图2，在 $△ A B C$ 和 $△ A E F$ 中， $A B = A C$ ， $A E = A F$ ， $∠ B A C = ∠ E A F = 120 °$ ，连接 $B E$ ， $C F$ ，延长 $B E$ ， $F C$ 交于点 $D$ ．请猜想 $B E$ 与 $C F$ 的数量关系及 $∠ B D C$ 的度数，并说明理由．

查看试题解析