【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略10 弧长和扇形的面积
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 已知一个扇形的圆心角是150°,半径是3,则该扇形的弧长为( )A、 B、 C、 D、2. 已知一个扇形的面积是 , 弧长是 , 则这个扇形的半径为( )A、24 B、22 C、12 D、63. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
 A、 B、 C、2π D、4. 如图,为了美化校园,学校在一块边角空地建造了一个扇形花圃,扇形圆心角∠AOB=120°,半径OA为3m,那么花圃的面积为( )
A、 B、 C、2π D、4. 如图,为了美化校园,学校在一块边角空地建造了一个扇形花圃,扇形圆心角∠AOB=120°,半径OA为3m,那么花圃的面积为( ) A、6πm2 B、3πm2 C、2πm2 D、πm25. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )
A、6πm2 B、3πm2 C、2πm2 D、πm25. 如图是某款“不倒翁”的示意图, , 分别与所在圆相切于点 , . 若该圆半径是 , , 则的长是( )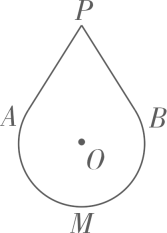 A、 B、 C、 D、6. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( )
A、 B、 C、 D、6. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( ) A、 B、 C、 D、7. 如图是小李上学用的自行车,型号是24英寸(车轮的直径为24英寸,1英寸=2.54厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°安装时向车轮外延伸2.52厘米,那么预计需要的铁皮面积约是( )
A、 B、 C、 D、7. 如图是小李上学用的自行车,型号是24英寸(车轮的直径为24英寸,1英寸=2.54厘米),为了防止在下雨天骑车时的泥水溅到身上,他想在自行车两轮的阴影部分两侧装上挡水的铁皮(两个阴影部分分别是以C、D为圆心的两个扇形),量出四边形ABCD中∠DAB=125°、∠ABC=115°安装时向车轮外延伸2.52厘米,那么预计需要的铁皮面积约是( ) A、1141平方厘米 B、2281平方厘米 C、3752平方厘米 D、4000平方厘米8. 如图,已知 , 的弧长之差为 , , 则的长为( )
A、1141平方厘米 B、2281平方厘米 C、3752平方厘米 D、4000平方厘米8. 如图,已知 , 的弧长之差为 , , 则的长为( )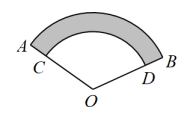 A、 B、 C、6 D、39. 如图,在扇形中, , 半径 , 将扇形沿过点的直线折叠,使点恰好落在上的点处,折痕为 , 则阴影部分的面积为( )
A、 B、 C、6 D、39. 如图,在扇形中, , 半径 , 将扇形沿过点的直线折叠,使点恰好落在上的点处,折痕为 , 则阴影部分的面积为( ) A、 B、 C、 D、10. 如图,在中, , , , 点为的中点,以点为圆心作圆心角为的扇形 , 点恰在弧上,则图中阴影部分的面积为( )
A、 B、 C、 D、10. 如图,在中, , , , 点为的中点,以点为圆心作圆心角为的扇形 , 点恰在弧上,则图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若扇形的圆心角为 , 半径为 , 则它的弧长是 .12. 已知圆弧的度数为 , 弧长为 , 则圆的半径是.13. 已知扇形的半径为 , 弧长是 , 则扇形的面积是.14. 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,OC=2,则图中的阴影部分的面积是 .
 15. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 .
15. 把量角器和含角的三角板按如图1方式摆放,将其抽象为图2:若与相切于点E, , . 则阴影部分的面积为 . 16. 如图,在半径为6,圆心角为90°的扇形OAB中,=2 , 点D是半径OB的中点,点P从点D出发,沿D→O→A的方向运动到A的过程中(包括D,A点),线段BP,CP与所围成的区域(如图中阴影部分)面积的最小值为 .
16. 如图,在半径为6,圆心角为90°的扇形OAB中,=2 , 点D是半径OB的中点,点P从点D出发,沿D→O→A的方向运动到A的过程中(包括D,A点),线段BP,CP与所围成的区域(如图中阴影部分)面积的最小值为 .
三、解答题
-
17. 如图,已知扇形AOB的圆心角为120°,半径OA为6cm.求扇形AOB的弧长和面积.
 18. 已知:如图,C,D是以为直径的半圆周的三等分点,.求阴影部分的面积?
18. 已知:如图,C,D是以为直径的半圆周的三等分点,.求阴影部分的面积? 19. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
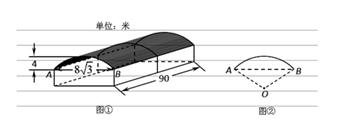
19. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长. 20. 为保护共享单车,图①是某工厂门口修建的存放自行车的车棚示意图(尺寸如 图所示).车棚顶部是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部截面的示 意图,弧 AB 所在圆的圆心为 O.车棚顶部是用铝合金覆盖的,求所用铝合金的面积
20. 为保护共享单车,图①是某工厂门口修建的存放自行车的车棚示意图(尺寸如 图所示).车棚顶部是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部截面的示 意图,弧 AB 所在圆的圆心为 O.车棚顶部是用铝合金覆盖的,求所用铝合金的面积(不考虑接缝等因素,计算结果保留 π).
 21. 在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎.如图,为圆的直径,是的一条弦,为弧的中点,作于点 , 交的延长线于点 , 连接 .
21. 在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎.如图,为圆的直径,是的一条弦,为弧的中点,作于点 , 交的延长线于点 , 连接 .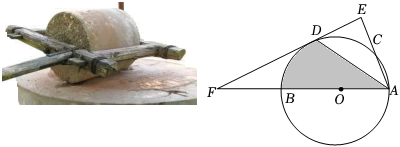 (1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留22. 如图,在Rt中,为AC边上一点,连结OB.以OC为半径的半圆与AB边相切于点 , 交AC边于点.
(1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留22. 如图,在Rt中,为AC边上一点,连结OB.以OC为半径的半圆与AB边相切于点 , 交AC边于点.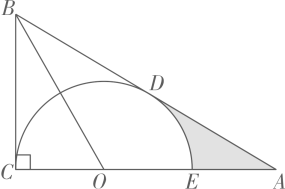 (1)、求证:.(2)、若.
(1)、求证:.(2)、若.①求半圆的半径.
②求图中阴影部分的面积.
23. 项目化学习:车轮的形状.【问题提出】车轮为什么要做成圆形, 这里面有什么数学原理?
(1)、【合作探究】

探究 组:如图1,圆形车轮半径为 ,其车轮轴心 到地面的距离始终为 .
探究 组:如图2,正方形车轮的轴心为 ,若正方形的边长为 ,求车轮轴心 最高点与最低点的高度差.
探究 组:如图3, 有一个破损的圆形车轮, 半径为 ,破损部分是一个弓形,其所对圆心角为 ,其车轮轴心为 ,让车轮在地上无滑动地滚动一周,求点 经过的路程.探究发现:车辆的平稳关键看车轮轴心是否稳定.
(2)、【拓展延伸】如图4,分别以正三角形的三个顶点 为圆心,以正三角形的边长为半径作 圆弧,这个曲线图形叫做“莱洛三角形”.
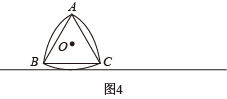
探究 组:使 “莱洛三角形” 沿水平方向向右滚动,在滚动过程中,其每时每刻都有 “最高点”,“中心点” 也在不断移动位置,那么在 “莱洛三角形” 滚动一周的过程中,其“最高点”和“中心点”所形成的图案大致是 .
延伸发现:“莱洛三角形”在滚动时始终位于一组平行线之间,因此放在其上的物体也能够保持平衡,但其车轴中心 并不稳定.