2023-2024学年高中数学人教A版必修二 8.6 空间直线、平面的垂直 同步练习
试卷更新日期:2023-12-12 类型:同步测试
一、选择题
-
1. 已知 , 表示两条不同的直线,表示平面,则下列说法正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则2. 已知是不重合的三条直线,是不重合的三个平面,则( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , , , , 则3. 已知 , 是平面, , 是直线.下列命题中不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则4. 在矩形中, , , 现将沿折起成 , 折起过程中,当时,四面体体积为( )
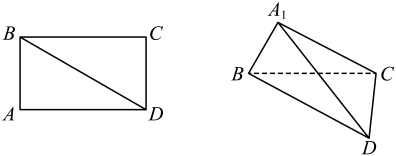 A、2 B、 C、 D、5. 在空间中,是不重合的直线,是不重合的平面,则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 则6. 已知平面 , 直线 , 直线不在平面内,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 已知空间中三个互不相同的平面、、 , 两条不同的直线a、b , 下列命题正确的是( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , , 则8. 设为平面,为直线,则的一个充分条件是A、 B、 C、 D、9. 点、在以为直径的球的表面上,且 , , 已知球的表面积是 , 下列说法中正确的个数是( )
A、2 B、 C、 D、5. 在空间中,是不重合的直线,是不重合的平面,则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 则6. 已知平面 , 直线 , 直线不在平面内,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 已知空间中三个互不相同的平面、、 , 两条不同的直线a、b , 下列命题正确的是( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , , 则8. 设为平面,为直线,则的一个充分条件是A、 B、 C、 D、9. 点、在以为直径的球的表面上,且 , , 已知球的表面积是 , 下列说法中正确的个数是( )①平面;②平面平面;③ .
A、0 B、1 C、2 D、310. 如图,已知棱长为的正方体中,点在正方体的棱、、上运动,平面 , 垂足为 , 则点形成图形中的各线段长度之和是( )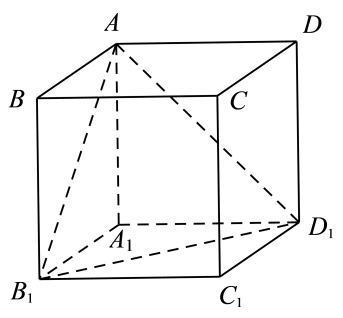 A、2 B、 C、 D、11. 设 , 是两条不同的直线, , 是两个不同的平面,则下列结论不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , , 与相交,则12. 已知m,n是不同的直线, , 是不同的平面,下列命题中,正确的是( )A、若∥ , ∥ , 则∥ B、若 , , 则 C、若 , ∥ , 且 , 则 D、若 , , 且 , 则13. 已知直线 , , 和平面 , 则下列命题正确的是( )A、若 , , 则 B、若 , , , , 则 C、若 , , , , 则 D、若 , , 则14. 如图,在正四棱台中, , 则与平面所成角的大小为( )
A、2 B、 C、 D、11. 设 , 是两条不同的直线, , 是两个不同的平面,则下列结论不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , , 与相交,则12. 已知m,n是不同的直线, , 是不同的平面,下列命题中,正确的是( )A、若∥ , ∥ , 则∥ B、若 , , 则 C、若 , ∥ , 且 , 则 D、若 , , 且 , 则13. 已知直线 , , 和平面 , 则下列命题正确的是( )A、若 , , 则 B、若 , , , , 则 C、若 , , , , 则 D、若 , , 则14. 如图,在正四棱台中, , 则与平面所成角的大小为( ) A、 B、 C、 D、15. 如图,在正方体中, , 为正方体内(含边界)不重合的两个动点,下列结论错误的是( )
A、 B、 C、 D、15. 如图,在正方体中, , 为正方体内(含边界)不重合的两个动点,下列结论错误的是( ) A、若 , , 则 B、若 , , 则平面平面 C、若 , , 则 D、若 , , 则平面
A、若 , , 则 B、若 , , 则平面平面 C、若 , , 则 D、若 , , 则平面二、多项选择题
-
16. 设是两条不同的直线,是两个不同的平面,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则17. 如图,以等腰直角三角形的斜边上的高为折痕,翻折和 , 使得平面平面.下列结论正确的是( )
 A、 B、是等边三角形 C、三棱锥是正三棱锥 D、平面平面18. 在空间中,设为两条不同的直线, , 为两个不同的平面,则下列正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , , 则 D、若 , , , 则19. 如图,棱长为的正方体中,点 , 分别是棱 , 的中点,则( )
A、 B、是等边三角形 C、三棱锥是正三棱锥 D、平面平面18. 在空间中,设为两条不同的直线, , 为两个不同的平面,则下列正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , , 则 D、若 , , , 则19. 如图,棱长为的正方体中,点 , 分别是棱 , 的中点,则( ) A、直线平面 B、直线平面 C、 D、过 , , 三点的平面截正方体的截面面积为20. 点在以为直径的球的表面上,且 , , 已知球的表面积是 , 设直线和所成角的大小为 , 直线和平面所成角的大小为 , 四面体内切球半径为 , 下列说法中正确的个数是( )A、平面 B、平面平面 C、 D、sinα=cos
A、直线平面 B、直线平面 C、 D、过 , , 三点的平面截正方体的截面面积为20. 点在以为直径的球的表面上,且 , , 已知球的表面积是 , 设直线和所成角的大小为 , 直线和平面所成角的大小为 , 四面体内切球半径为 , 下列说法中正确的个数是( )A、平面 B、平面平面 C、 D、sinα=cos三、填空题
-
21. 如图,在三棱锥中,平面 , , 则以此三棱锥的棱为边所构成的三角形中,直角三角形的个数有个.
 22. 已知 , 是平面 外的两条不同直线.给出下列三个论断:
22. 已知 , 是平面 外的两条不同直线.给出下列三个论断:① ;
② ;
③ .
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: .
23. 已知 , 表示直线, , , 表示平面.①若 , , , 则;
②若 , 垂直于内任意一条直线,则;
③若 , , , 则;
④若 , , , 则
上述命题中,正确命题的序号是.
24. 如图所示,在四棱锥P−ABCD中,PA⊥底面ABCD,且底面各边都相等, , M是PC上的一动点,当点M满足时,平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可) 25. 已知三个互不重合的平面α,β,γ,且直线m , n不重合,由下列条件:
25. 已知三个互不重合的平面α,β,γ,且直线m , n不重合,由下列条件:①m⊥n , m⊥β;②n⊂α,α∥β;③α⊥γ,β⊥γ,n⊂α;
能推得n∥β的条件是 .
四、解答题
-
26. 四棱锥的底面为正方形,为的中点.
 (1)、证明:平面;(2)、若平面 , 证明: .27. 如图,已知平面平面 , 四边形是矩形, , 点 , 分别是 , 的中点.
(1)、证明:平面;(2)、若平面 , 证明: .27. 如图,已知平面平面 , 四边形是矩形, , 点 , 分别是 , 的中点.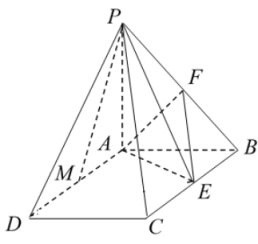 (1)、若点为线段中点,求证:平面;(2)、求证:平面.28. 如图,在四棱锥中,底面ABCD是边长为4的菱形, , , , , 点M、N分别是AB、CD的中点.
(1)、若点为线段中点,求证:平面;(2)、求证:平面.28. 如图,在四棱锥中,底面ABCD是边长为4的菱形, , , , , 点M、N分别是AB、CD的中点.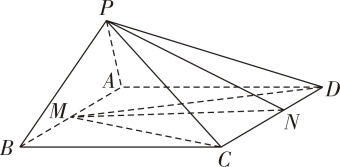 (1)、求证:平面PAB;(2)、求四面体PMND的体积.29. 如图,四棱锥的底面ABCD是边长为2的正方形, , 平面平面ABCD , 平面平面ABCD , E为PD中点.
(1)、求证:平面PAB;(2)、求四面体PMND的体积.29. 如图,四棱锥的底面ABCD是边长为2的正方形, , 平面平面ABCD , 平面平面ABCD , E为PD中点.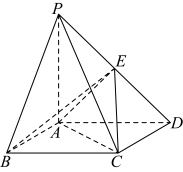 (1)、证明:;(2)、若F为棱PB上的点,求点F到平面ACE的距离.30. 如图,在四棱锥中,底面为平行四边形, , , , , , 为棱的中点.
(1)、证明:;(2)、若F为棱PB上的点,求点F到平面ACE的距离.30. 如图,在四棱锥中,底面为平行四边形, , , , , , 为棱的中点.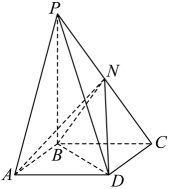
条件①:;
条件②:平面平面.
从条件①和条件②这两个条件中选择一个作为已知,完成下列问题:
(1)、求证:;(2)、若点在线段上,且点到平面的距离为 , 求线段的长.注:如果选择条件①和条件②分别解答,按第一个解答计分.
31. 如图,四棱柱ABCDA1B1C1D1中,M是棱DD1上的一点,AA1⊥平面ABCD , AB∥DC , AB⊥AD , AA1=AB=2AD=2DC. (1)、若M是DD1的中点,证明:平面AMB⊥平面A1MB1;(2)、设四棱锥M-ABB1A1与四棱柱ABCD-A1B1C1D1的体积分别为V1与V2 , 求的值.32. 如图,在三棱锥中,底面为的中点, .
(1)、若M是DD1的中点,证明:平面AMB⊥平面A1MB1;(2)、设四棱锥M-ABB1A1与四棱柱ABCD-A1B1C1D1的体积分别为V1与V2 , 求的值.32. 如图,在三棱锥中,底面为的中点, .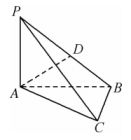 (1)、求证:平面;(2)、求证:平面 .33. 如图,四棱锥的底面为正方形,为的中点.
(1)、求证:平面;(2)、求证:平面 .33. 如图,四棱锥的底面为正方形,为的中点.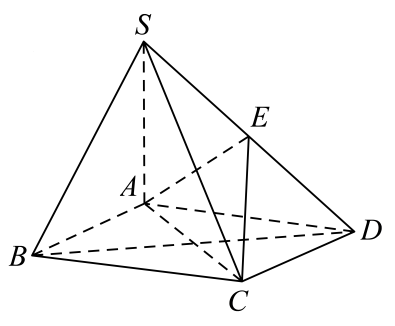 (1)、证明:平面;(2)、若平面 , 证明:.34. 如图,在四棱锥中,底面四边形为矩形,平面平面 , , , , 点为的中点.
(1)、证明:平面;(2)、若平面 , 证明:.34. 如图,在四棱锥中,底面四边形为矩形,平面平面 , , , , 点为的中点. (1)、求证:平面平面;(2)、求三棱锥的体积.35. 如图所示,在正方体中.(立体几何证明过程中不可使用向量法,否则不给分)
(1)、求证:平面平面;(2)、求三棱锥的体积.35. 如图所示,在正方体中.(立体几何证明过程中不可使用向量法,否则不给分)
求证:
(1)、直线平面;(2)、平面平面 .36. 如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且 , 点为棱上的点,平面与棱交于点 .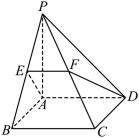 (1)、求证:;(2)、若 , , 求证平面平面 .
(1)、求证:;(2)、若 , , 求证平面平面 .