【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略8 圆内四边形
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 下列命题中,是真命题的是( )A、平分弦的直径垂直于弦 B、相等圆周角所对的弧相等 C、任意三个点确定一个圆 D、圆内接平行四边形必为矩形2. 如图,四边形是的内接四边形,的半径为2, , 则为( )
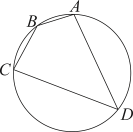 A、 B、 C、 D、3. 圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( )A、1:2:3:4 B、4:2:3:1 C、4:3:1:2 D、4:1:3:24. 如图,四边形ABCD内接于圆O,∠DCE=65°,则∠A的度数为( )
A、 B、 C、 D、3. 圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( )A、1:2:3:4 B、4:2:3:1 C、4:3:1:2 D、4:1:3:24. 如图,四边形ABCD内接于圆O,∠DCE=65°,则∠A的度数为( ) A、112° B、68° C、65° D、52°5. 如图,四边形 是 的内接四边形, ,则 的度数为( )
A、112° B、68° C、65° D、52°5. 如图,四边形 是 的内接四边形, ,则 的度数为( ) A、70° B、90° C、100° D、110°6. 在中,点 , , , 都在圆周上, , , 则的度数为( )
A、70° B、90° C、100° D、110°6. 在中,点 , , , 都在圆周上, , , 则的度数为( )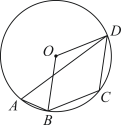 A、 B、 C、 D、7. 用破损量角器按如图方式测量∠ABC的度数,让∠ABC的顶点恰好在量角器圆弧上,两边分别经过圆弧上的A,C两点.若点A,C对应的刻度分别为55°,135°,则∠ABC的度数为( ).
A、 B、 C、 D、7. 用破损量角器按如图方式测量∠ABC的度数,让∠ABC的顶点恰好在量角器圆弧上,两边分别经过圆弧上的A,C两点.若点A,C对应的刻度分别为55°,135°,则∠ABC的度数为( ). A、130° B、135° C、140° D、145°8. 如图,四边形内接于 , , , , 点为的中点,则线段的长为( )
A、130° B、135° C、140° D、145°8. 如图,四边形内接于 , , , , 点为的中点,则线段的长为( )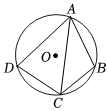 A、 B、 C、 D、9. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
A、 B、 C、 D、9. 如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )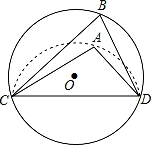 A、100° B、80° C、60° D、50°10. 如图,等腰Rt△ABC中,∠B=90°.D是AC边上的中点,过B,D两点的圆与边AB,BC分别交于点E,F,若△AED与△BEF的面积之比为2:3,DE=3,则BE的长为( )
A、100° B、80° C、60° D、50°10. 如图,等腰Rt△ABC中,∠B=90°.D是AC边上的中点,过B,D两点的圆与边AB,BC分别交于点E,F,若△AED与△BEF的面积之比为2:3,DE=3,则BE的长为( )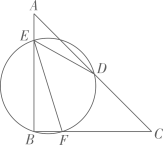 A、 B、 C、4 D、3
A、 B、 C、4 D、3二、填空题
-
11. 如图,四边形内接于圆 , 若 , 则的度数是.
 12. 在圆内接四边形ABCD中, , 则的度数为.13. 如图,四边形ABCD是的内接四边形,BE是的直径,连结CE,若 , 则 度.
12. 在圆内接四边形ABCD中, , 则的度数为.13. 如图,四边形ABCD是的内接四边形,BE是的直径,连结CE,若 , 则 度. 14. 如图,四边形的顶点、、在上,若 , 则.
14. 如图,四边形的顶点、、在上,若 , 则. 15. 若⊙O中,弦AB的长度是半径的倍,则弦AB所对圆周角的度数为°.16. 如图,在平面直角坐标系xOy中,点B在x轴正半轴上,点D在y轴正半轴上,⊙C经过A,B,D,O四点,∠OAB=120°,OB=4 , 则点D的坐标是 .
15. 若⊙O中,弦AB的长度是半径的倍,则弦AB所对圆周角的度数为°.16. 如图,在平面直角坐标系xOy中,点B在x轴正半轴上,点D在y轴正半轴上,⊙C经过A,B,D,O四点,∠OAB=120°,OB=4 , 则点D的坐标是 .
三、解答题
-
17. 已知四边形ABCD内接于⊙O,= , ∠ADC=120°,求证:△ABC是等边三角形.
 18.
18.如图,四边形ABCD内接于⊙O,BC的延长线与AD的延长线相交于点E,且DC=DE.求证:∠A=∠AEB.
 19.
19.如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD•DC=PA•BC.
 20. 如图,在三角形ABC中, ∠ C=90°,I是内心,直线BI与AC交于点D,过点D作DE//AI与BC交于点E,直线EI与AB交于点F.证明:DF ⊥ AI.
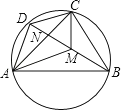
20. 如图,在三角形ABC中, ∠ C=90°,I是内心,直线BI与AC交于点D,过点D作DE//AI与BC交于点E,直线EI与AB交于点F.证明:DF ⊥ AI.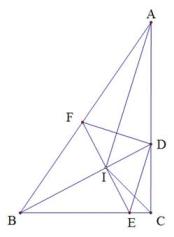 21. 如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
21. 如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.求证:(1)M为BD的中点;(2) .
 22. 如图,圆中延长弦 , 交于点 , 连接 , , , .
22. 如图,圆中延长弦 , 交于点 , 连接 , , , . (1)、若 , , 求的度数;(2)、若 , , , 判断 , , 满足什么数量关系时,?请说明理由.23. 定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形.
(1)、若 , , 求的度数;(2)、若 , , , 判断 , , 满足什么数量关系时,?请说明理由.23. 定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形. (1)、如图1,点C是的中点,∠DAB是所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.(2)、如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.(3)、如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.
(1)、如图1,点C是的中点,∠DAB是所对的圆周角,AD>AB,连结AC、DC、CB,试说明△ACB与△ACD是偏等三角形.(2)、如图2,△ABC与△DEF是偏等三角形,其中∠A=∠D,AC=DF,BC=EF,则∠B+∠E=.请填写结论,并说明理由.(3)、如图3,△ABC内接于⊙O,AC=4,∠A=30°,∠B=105°,若点D在⊙O上,且△ADC与△ABC是偏等三角形,AD>CD,求AD的值.