浙教版数学七年级上册期末冲刺满分攻略8 实数的运算

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知实数a，b，c，且a＜b＜0＜c，则化简|a-b|-|c-a|正确的是（）

A、a-b B、b-c C、c-a D、a-b+c

查看试题解析
2. 下列运算正确的是（）

A、− $2 \sqrt{3} - \sqrt{3}$ =±3 B、 $\sqrt{27}$ =3 C、− $\sqrt{9}$ =−3 D、−3²=9

查看试题解析
3. 化简 $\sqrt{3} - | \sqrt{3} - 1 |$ 的结果是（）

A、 $2 \sqrt{3}$ B、1 C、2 D、-1

查看试题解析
4. 下列说法正确的个数是（）
①最小的负整数是﹣1；②所有无理数都能用数轴上的点表示；③当a≤0时，|a|＝﹣a成立；④两个无理数的和可能为有理数.

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列说法错误的是（）

A、 $\sqrt{81}$ 的平方根是 $\pm 3$ B、 ${(- 1)}^{2012}$ 是最小的正整数 C、两个无理数的和一定是无理数 D、实数与数轴上的点——对应

查看试题解析
6. 实数 $a$ ， $b$ 在数轴上的位置如图所示，则下面的关系式中正确的个数为（）
① $a + b > 0$ ；② $b - a > 0$ ；③ $\frac{1}{a} > \frac{1}{b}$ ；④ $| a | < | b |$ .

A、4 B、3 C、2 D、1

查看试题解析
7. 有下列说法：①在1和2之间的无理数有且只有 $\sqrt{2} ， \sqrt{3}$ 这两个；②实数与数轴上的点一一对应；③两个无理数的积一定是无理数；④ $\frac{π}{2}$ 是分数.其中正确的为（）

A、①②③④ B、①②④ C、②④ D、②

查看试题解析
8. 实数a、b在数轴上的位置如图所示，则下列各式正确的是（）

A、 $a + b > 0$ B、 $a - b < 0$ C、 $a b > 0$ D、 $| b | > a$

查看试题解析
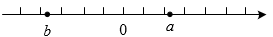9. 下列计算正确的是（）

A、 $- 2 + (- 6) = 8$ B、 ${(- 2)}^{3} = - 6$ C、 $(- 2) \div \frac{1}{4} \times (- 2) = 4$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
10. 下列说法：①有理数与数轴上的点一一对应；②1.4×10⁴精确到千位；③两个无理数的积一定为无理数；④立方和立方根都等于它本身的数是0或±1．其中正确的是（）

A、①② B、①③ C、③④ D、②④

查看试题解析

二、填空题

11. 写出两个无理数，使它们的和为2 ．

查看试题解析
12. 用“*”表示一种新运算：对于任意正实数a*b＝ $\sqrt{a^{2} + b}$ ，例如10*21＝ $\sqrt{1 0^{2} + 21}$ ＝11，则 $\sqrt{13}$ *（ $\sqrt{7}$ *2）的运算结果为 .

查看试题解析
13. 已知 $7 + \sqrt{13}$ 的整数部分是 $m ， \sqrt{13}$ 的小数部分是n，则 $m + n =$ .

查看试题解析
14. 已知m与n互为相反数，c与d互为倒数，a是 $\sqrt{5}$ 的整数部分，则 $\sqrt{c d}$ ＋2(m＋n)－a的值是．

查看试题解析
15. 如图，是一个计算程序，若输入的数为 $\sqrt{7}$ ，则输出的结果应为.

查看试题解析

16. 如图，将 1、

\sqrt{2} ， \sqrt{3}

，三个数按图中方式排列，若规定（a，b）表示第

a

排第

b

列的数，（3，2）为第 3 排第 2 列的数为

\sqrt{2}

，则（8，2）与（100，100）表示的两个数的积是．

					1	第一排
				$\sqrt{3}$	$\sqrt{2}$	第二排
			$\sqrt{3}$	$\sqrt{2}$	$1$	第三排
		$1$	$\sqrt{3}$	$\sqrt{2}$	$1$	第四排
	$\sqrt{3}$	$\sqrt{2}$	$1$	$\sqrt{3}$	$\sqrt{2}$	第五排
……	第五列	第四列	第三列	第二列	第一列	……

查看试题解析

三、解答题

17. 计算：

(1)、 $42 \times (- \frac{2}{3}) + (- \frac{3}{4}) \div (- \frac{1}{8})$

(2)、 $- 3^{2} \times (\frac{1}{2} - \frac{1}{3}) + \sqrt{9} - | - 2 |$

查看试题解析
18. 计算：

(1)、 $(- \frac{1}{2} + \frac{2}{3}) \times$ $\sqrt{36}$ ；

(2)、 $6 \times | - 3 | - 2^{3} \div (- 1)^{2022}$ .

查看试题解析
19. 已知a是 $\sqrt{7}$ 的整数部分， $b^{2} = 9$ ， c是－3的倒数．

(1)、填空：a＝， b＝， c＝；

(2)、若实数d ， e互为相反数，求 $2 d + 2 e - b c + c^{a}$ ．

查看试题解析
20. 数学活动课上，张老师说：“ $\sqrt{2}$ 是无理数，无理数就是无限不循环小数，同学们，你能把 $\sqrt{2}$ 的小数部分全部写出来吗？”大家议论纷纷，晶晶同学说：“要把它的小数部分全部写出来是非常难的，但我们可以用（ $\sqrt{2}$ -1）表示它的小数部分．”张老师说：“晶晶同学的说法是正确的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．”请你解答：

(1)、 $\sqrt{5}$ 的整数部分是，小数部分是．

(2)、已知 $8 + \sqrt{3} = x + y$ ，其中x是一个整数，且0＜y＜1，请求出 $3 x + (y - \sqrt{3})^{2020}$ 的值．

查看试题解析
21. 已知x，y为有理数，如果规定一种运算“@”，即x@y＝xy+x+y，试根据这种运算完成下列各题.

(1)、求2@4；

(2)、任意选择两个有理数x，y，分别计算x@y和y@x，并比较两个运算结果，判断此运算满足什么运算律？

(3)、求（2@ $\sqrt{5}$ ）@（-3）.

查看试题解析
22. 阅读材料，解答下面的问题：
$∵$ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，

$∴$ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ ．

(1)、求 $\sqrt{6}$ 的整数部分．

(2)、已知 $5 + \sqrt{6}$ 的小数部分是 $a$ ， $5 - \sqrt{6}$ 的小数部分是 $b$ ，求 ${(a + b)}^{2021}$ 的值．

查看试题解析
23. [阅读材料]
∵ $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，

∴1＜ $\sqrt{5}$ -1＜2．

∴ $\sqrt{5}$ -1的整数部分为1．

∴ $\sqrt{5}$ -1的小数部分为 $\sqrt{5}$ -2．

[解决问题]

(1)、填空： $\sqrt{91}$ 的小数部分是．

(2)、已知a是 $\sqrt{21}$ 的整数部分，b是 $\sqrt{21}$ 的小数部分，求代数式（-a）³+（b+4）²的值．

查看试题解析
24. 观察下列一组算式的特征及运算结果，探索规律：
(1) $\sqrt{1 \times 5 + 4} = \sqrt{9} = 3$ ，
(2) $\sqrt{2 \times 6 + 4} = \sqrt{16} = 4$ ，
(3) $\sqrt{3 \times 7 + 4} = \sqrt{25} = 5$ ，
(4) $\sqrt{4 \times 8 + 4} = \sqrt{36} = 6$ .

(1)、观察算式规律，计算 $\sqrt{5 \times 9 + 4} =$ ； $\sqrt{19 \times 23 + 4} =$ .

(2)、用含正整 $n$ 的式子表示上述算式的规律：.

(3)、计算： $\sqrt{1 \times 5 + 4} - \sqrt{2 \times 6 + 4} + \sqrt{3 \times 7 + 4} - \sqrt{4 \times 8 + 4} + ⋯ + \sqrt{2021 \times 2025 + 4}$ .

查看试题解析