【北师大版】2023-2024学年数学九年级(上)期末仿真模拟试题(二)
试卷更新日期:2023-12-12 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列图形中,主视图为矩形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在四边形ABCD中,∠A=∠B=90°,AB=BC=4,AD=3,E是边AB上一点,且∠DCE=45°,则DE的长度是( )
2. 如图,在四边形ABCD中,∠A=∠B=90°,AB=BC=4,AD=3,E是边AB上一点,且∠DCE=45°,则DE的长度是( ) A、3.2 B、3.4 C、3.6 D、43. 如图,正方形ABCD和长方形AEFG的面积相等,且四边形BEFH也是正方形,欧几里得在《几何原本》中利用该图得到了:.设 , .若 , 则图中阴影部分的周长是( )
A、3.2 B、3.4 C、3.6 D、43. 如图,正方形ABCD和长方形AEFG的面积相等,且四边形BEFH也是正方形,欧几里得在《几何原本》中利用该图得到了:.设 , .若 , 则图中阴影部分的周长是( ) A、6 B、8 C、10 D、204. 如图,把一块长为 , 宽为的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 , 设剪去小正方形的边长为 , 则所列方程正确的为( )
A、6 B、8 C、10 D、204. 如图,把一块长为 , 宽为的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为 , 设剪去小正方形的边长为 , 则所列方程正确的为( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中,已知 , , 与位似,原点O是位似中心.若 , 则点F的坐标是( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中,已知 , , 与位似,原点O是位似中心.若 , 则点F的坐标是( ) A、 B、 C、 D、6. 关于反比例函数y= , 下列说法不正确的是( )A、函数图象分别位于第二、四象限 B、函数图象关于原点成中心对称 C、函数图象经过点(1,1) D、当x>0时,y随x的增大而减小7. 某学校在八年级开设了数学史、诗词赏析、陶艺三门课程,若小波和小睿两名同学每人随机选择其中一门课程,则小波和小睿选到同一门课程的概率是( )A、 B、 C、 D、8. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
A、 B、 C、 D、6. 关于反比例函数y= , 下列说法不正确的是( )A、函数图象分别位于第二、四象限 B、函数图象关于原点成中心对称 C、函数图象经过点(1,1) D、当x>0时,y随x的增大而减小7. 某学校在八年级开设了数学史、诗词赏析、陶艺三门课程,若小波和小睿两名同学每人随机选择其中一门课程,则小波和小睿选到同一门课程的概率是( )A、 B、 C、 D、8. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、抛一个质地均匀的正六面体骰子,向上的面点数是5 C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” D、抛一枚硬币,出现反面的概率9. 如图所示,电路连接完好,且各元件工作正常.随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是( )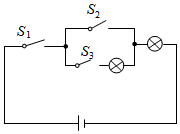 A、0 B、 C、 D、10. 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 , 对角线长为 , 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )
A、0 B、 C、 D、10. 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具,此时测得 , 对角线长为 , 改变教具的形状成为图2所示的正方形,则正方形的对角线长为( )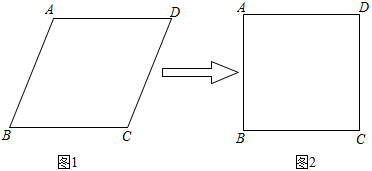 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分))
-
11. 如图,已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=8,BD=3,则DF的值是 .
 12. 如图,在边长为7的等边△ABC中,D、E分别在边AC、BC上,AD=2CD,CE=2BE,连结AE、BD交于点P,则CP的长为 .
12. 如图,在边长为7的等边△ABC中,D、E分别在边AC、BC上,AD=2CD,CE=2BE,连结AE、BD交于点P,则CP的长为 . 13. 如图,△ABC的面积为40cm2 , DE=2AE , CD=3BD , 则四边形BDEF的面积等于cm2 .
13. 如图,△ABC的面积为40cm2 , DE=2AE , CD=3BD , 则四边形BDEF的面积等于cm2 .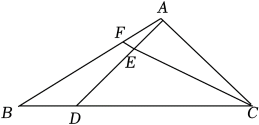 14. 如图是小孔成像原理的示意图, , , . 若物体的高度为 , 则像的高度是.
14. 如图是小孔成像原理的示意图, , , . 若物体的高度为 , 则像的高度是.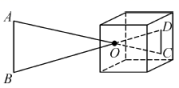 15. 如图,已知一次函数y=2x+4的图象与反比例函数y=的图象交于A,B两点,点B的横坐标是1,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积是 .
15. 如图,已知一次函数y=2x+4的图象与反比例函数y=的图象交于A,B两点,点B的横坐标是1,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积是 .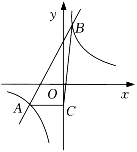
三、解答题(共7题,共55分)
-
16. 用公式法解方程:2x2-2x-1=017. 解方程: .18. 为落实“双减”,进一步深化白云区“数学提升工程”,提升学生数学核心素养,2021年12月3日开展“双减”背景下白云区初中数学提升工程成果展示现场会,其中活动型作业展示包括以下项目:①数独挑战;②数学谜语;③一笔画;④24点;⑤玩转魔方.为了解学生最喜爱的项目,随机抽取若干名学生进行调查,将调查结果绘制成两个不完整的统计图,如图:
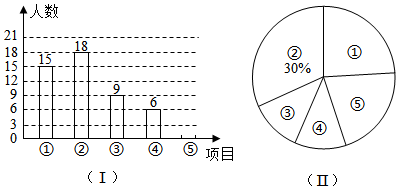 (1)、本次随机抽查的学生人数为 ▲ 人,补全图(Ⅰ);(2)、参加活动的学生共有500名,可估计出其中最喜爱①数独挑战的学生人数为人,图(Ⅱ)中扇形①的圆心角度数为度;(3)、计划在①,②,③,④四项活动中随机选取两项作为重点直播项日,请用列表或画树状图的方法,求恰好选中①,④这两项活动的概率19. 据统计,假期第一天前海欢乐港湾摩天轮的游客人数为5000人次,第三天游客人数达到7200人次.(1)、求游客人数从假期第一天到第三天的平均日增长率;(2)、据悉,景区附近商店推出了前海旅游纪念章,每个纪念章的成本为5元,当售价为10元时,平均每天可售出500个,为了让游客尽可能得到优惠,商店决定降价销售.市场调查发现,售价每降低1元,平均每天可多售出200个,若要使每天销售旅游纪念章获利2800元,则售价应降低多少元?20. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下:
(1)、本次随机抽查的学生人数为 ▲ 人,补全图(Ⅰ);(2)、参加活动的学生共有500名,可估计出其中最喜爱①数独挑战的学生人数为人,图(Ⅱ)中扇形①的圆心角度数为度;(3)、计划在①,②,③,④四项活动中随机选取两项作为重点直播项日,请用列表或画树状图的方法,求恰好选中①,④这两项活动的概率19. 据统计,假期第一天前海欢乐港湾摩天轮的游客人数为5000人次,第三天游客人数达到7200人次.(1)、求游客人数从假期第一天到第三天的平均日增长率;(2)、据悉,景区附近商店推出了前海旅游纪念章,每个纪念章的成本为5元,当售价为10元时,平均每天可售出500个,为了让游客尽可能得到优惠,商店决定降价销售.市场调查发现,售价每降低1元,平均每天可多售出200个,若要使每天销售旅游纪念章获利2800元,则售价应降低多少元?20. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下: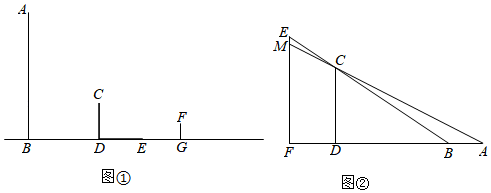
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
(1)、已知榕树CD在路灯下的影子为DE,请画出榕树FG在路灯下的影子GH;(2)、如图①,若榕树CD的高度为3.6米,其离路灯的距离BD为6米,两棵榕树的影长DE,GH均为4米,两棵树之间的距离DG为6米,求榕树FG的高度;(3)、无论太阳光还是点光源,其本质与视线问题相同.日常生活中我们也可以直接利用视线解决问题.如图②,建筑物CD高为50米,建筑物MF上有一个广告牌EM,合计总高度EF为70米,两座建筑物之间的直线距离FD为30米.一个观测者(身高不计)先站在A处观测,发现能看见广告牌EM的底端M处,观测者沿着直线AF向前走了5米到B处观测,发现刚好看到广告牌EM的顶端E处.则广告牌EM的高度为 米.21. 矩形中, , 点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.(1)、【特例证明】如图,当时,求证:;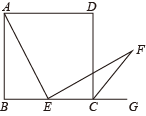 (2)、【类比探究】如图,当时,求的值(用含k的式子表示);
(2)、【类比探究】如图,当时,求的值(用含k的式子表示); (3)、【拓展运用】如图,当时,P为边CD上一点,连接AP,PF, , , 则BC的长为 .
(3)、【拓展运用】如图,当时,P为边CD上一点,连接AP,PF, , , 则BC的长为 . 22. 如图
22. 如图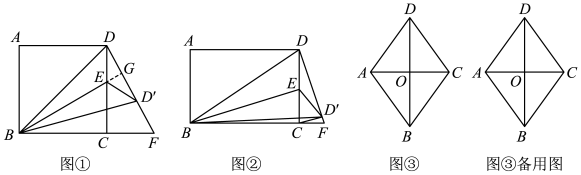 (1)、【探究发现】
(1)、【探究发现】如图①,已知四边形ABCD是正方形,点E为CD边上一点(不与端点重合),连接BE,作点D关于BE的对称点D',DD'的延长线与BC的延长线交于点F,连接BD′,D'E.
①小明探究发现:当点E在CD上移动时,△BCE≌△DCF.并给出如下不完整的证明过程,请帮他补充完整.
证明:延长BE交DF于点G.
②进一步探究发现,当点D′与点F重合时,∠CDF= ▲ °.
(2)、【类比迁移】如图②,四边形ABCD为矩形,点E为CD边上一点,连接BE,作点D关于BE的对称点D',DD′的延长线与BC的延长线交于点F,连接BD',CD',D'E.当CD'⊥DF,AB=2,BC=3时,求CD'的长;
(3)、【拓展应用】如图③,已知四边形ABCD为菱形,AD= , AC=2,点F为线段BD上一动点,将线段AD绕点A按顺时针方向旋转,当点D旋转后的对应点E落在菱形的边上(顶点除外)时,如果DF=EF,请直接写出此时OF的长.