天津市河北区2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2023-12-12 类型：期中考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）

A、3cm，4cm，8cm B、8cm，7cm，15cm C、5cm，5cm，11cm D、13cm，12cm，20cm

查看试题解析
3. 如图， $△ A B C$ 的边 $A C$ 上的高是（）

A、线段 $A E$ B、线段 $B A$ C、线段 $B D$ D、线段 $B C$

查看试题解析
4. 如图，a ， b ， c分别表示 $△ A B C$ 的三边长，则下面与 $△ A B C$ 一定全等的三角形是（）

A、① B、② C、③ D、④

查看试题解析
5. 一个多边形的每个外角都等于45°，则这个多边形的边数是（）

A、11 B、10 C、9 D、8

查看试题解析
6. 如图，已知 $△ A D C ≌ △ A E B$ ，且 $A C = 5$ ， $A D = 2$ ，则 $C E$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，在 $△ A B C$ 中， $D E$ 是 $A C$ 的垂直平分线， $A B = 5 c m$ ， $B C = 8 c m$ ，则 $△ A B D$ 的周长为（　　）

A、 $10 c m$ B、 $13 c m$ C、 $15 c m$ D、 $16 c m$

查看试题解析
8. 如图， $O P$ 平分 $∠ A O B$ ， $P A ⊥ O A$ ， $P B ⊥ O B$ ，垂足分别为A ， B ，下列结论中不一定成立的是（　　）

A、 $P A = P B$ B、 $P O$ 平分 $∠ A P B$ C、 $O A = O B$ D、 $A B$ 垂直平分 $O P$

查看试题解析
9. 如图所示的几何图形， $∠ A + ∠ B + ∠ C + ∠ D + ∠ E$ 的度数为（）

A、 $360 °$ B、 $270 °$ C、 $240 °$ D、 $180 °$

查看试题解析
10. 如图，在 $△ A B C$ 中， $B D$ 是 $A C$ 边上的高， $C E$ 是 $∠ A C B$ 的平分线， $B D$ ， $C E$ 交于点F ．若 $∠ A E C = 80 °$ ， $∠ B F C = 128 °$ ，则 $∠ A B C$ 的度数是（）

A、 $28 °$ B、 $38 °$ C、 $42 °$ D、 $62 °$

查看试题解析
11. 如图， $∠ A B C = 50 °$ ，点D ， E分别在射线 $B A$ ， $B C$ 上，将三角形 $B E D$ 沿着 $D E$ 折叠，若点B恰好落在射线 $D A$ 上的 $B^{'}$ 处，则 $∠ B E B^{'}$ 的度数是（）

A、 $50 °$ B、 $80 °$ C、 $100 °$ D、 $130 °$

查看试题解析
12. 如图， $O P$ 平分 $∠ M O N$ ， $P A ⊥ O N$ 于点 $A$ ，点 $Q$ 是射线 $O M$ 上的一个动点，若 $P A = 3$ ，则 $P Q$ 的最小值为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分．

13. 在平面直角坐标系中，点 $(m ， - 2)$ 与点 $(3 ， n)$ 关于x轴对称，则 $m + n =$ ．

查看试题解析
14. 如图， $A D ， A E$ 分别是 $Δ A B C$ 的高和角平分线，若 $∠ B = 30 °$ ， $∠ C = 50 °$ ，则 $∠ D A E$ 的度数为．

查看试题解析
15. 已知：如图， $△ A B C$ 的两个外角的平分线交于点P ，如果 $∠ A = 40 °$ ，则 $∠ B P C$ ．

查看试题解析
16. 如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度 $A C$ 与右边滑梯水平方向的长度 $D F$ 相等，这两个滑梯与地面夹角中 $∠ A B C = 35 °$ ，则 $∠ D F E =$ $°$ ．

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处．若∠A=26°，则∠CDE= ．

查看试题解析
18. 如图，△ABC中，点E是BC上的一点，EC=2BE，BD是边AC上的中线，若S_△_ABC=18，则S_△_ADF-S_△_BEF= ．

查看试题解析

三、解答题：本大题共6小题，共46分，解答应写出文字说明，演算步骤或证明过程．

19. 如图，在△ABC中， $∠ A = 35 °$ ， $∠ A B D = 35 °$ ， $∠ A C B = 80 °$ ，且CE平分 $∠ A C B$ ，求 $∠ B E C$ 的度数.

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 顶点的坐标分别是 $A (- 1 ， 3)$ ， $B (- 5 ， 1)$ ， $C (- 2 ， - 2)$ ．

(1)、画出 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ，并写出 $△ A^{'} B^{'} C^{'}$ 各顶点的坐标；

(2)、求出 $△ A B C$ 的面积．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B A C = 120 °$ ，点D是 $B C$ 上一点， $B D$ 的垂直平分线交 $A B$ 于点E ，将 $△ A C D$ 沿 $A D$ 折叠，点C恰好与点E重合，求 $∠ B$ 的度数．

查看试题解析
22. 如图，在△ABC中，∠BAC=90°，AB=AC ，直线MN经过点A ，过点B作BD⊥MN于D ，过C作CE⊥MN于E ．

(1)、求证：△ABD≌△CAE；

(2)、若BD=12cm，DE=20cm，求CE的长度．

查看试题解析
23. 已知△ABC中，∠B＝50°，∠C＝70°，AD是△ABC的角平分线，DE⊥AB于E点．

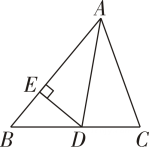(1)、求∠EDA的度数；

(2)、AB＝10，AC＝8，DE＝3，求S_△_ABC ．

查看试题解析
24. 如图，在△ABC中，AB＝AC＝18cm，BC＝10cm，∠B=∠C ， AD＝2BD ．如果点P在线段BC上以2cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．

(1)、若点 Q的运动速度与点 P的运动速度相等，经过2s后，△BPD与△CQP是否全等，请说明理由；

(2)、若点 Q的运动速度与点 P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

(3)、若点Q以（2）中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

查看试题解析