人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——13.1轴对称
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 下列图形中.轴对称图形有( )
 A、1个 B、2个 C、3个 D、4个2. 有无数条对称轴的图形是( )A、线段 B、等边三角形 C、正方形 D、圆3. 在如图的三角形纸片中,AB=8cm , BC=6cm , AC=5cm , 沿过点B的直线折叠这个三角形,使点C落在AB上的点E处,折痕为BD , 则△AED的周长为( )
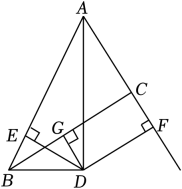
A、1个 B、2个 C、3个 D、4个2. 有无数条对称轴的图形是( )A、线段 B、等边三角形 C、正方形 D、圆3. 在如图的三角形纸片中,AB=8cm , BC=6cm , AC=5cm , 沿过点B的直线折叠这个三角形,使点C落在AB上的点E处,折痕为BD , 则△AED的周长为( ) A、5cm B、6cm C、7cm D、8cm4. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( )
A、5cm B、6cm C、7cm D、8cm4. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( ) A、 B、 C、 D、5. 如图,已知∠BAC的平分线与BC的垂直平分线相交于点D , DE⊥AB , DF⊥AC , 垂足分别为E , F , AB=6,AC=3,则BE=( )
A、 B、 C、 D、5. 如图,已知∠BAC的平分线与BC的垂直平分线相交于点D , DE⊥AB , DF⊥AC , 垂足分别为E , F , AB=6,AC=3,则BE=( ) A、6 B、3 C、2 D、1.56. 如图,直线、相交于点 , 点是直线外一点,在直线、上找一点 , 使为一个等腰三角形.满足条件的点有( )
A、6 B、3 C、2 D、1.56. 如图,直线、相交于点 , 点是直线外一点,在直线、上找一点 , 使为一个等腰三角形.满足条件的点有( )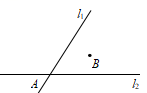 A、个 B、个 C、个 D、个7. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )
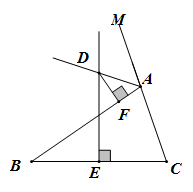
A、个 B、个 C、个 D、个7. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )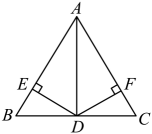 A、①④ B、②④ C、②③④ D、①②③④8. 如图,已知 , , 点P是AB上的一点,连结CP , 将沿CP所在直线折叠,点A落在点M处,连结MB , MD . 若 , , 则( )
A、①④ B、②④ C、②③④ D、①②③④8. 如图,已知 , , 点P是AB上的一点,连结CP , 将沿CP所在直线折叠,点A落在点M处,连结MB , MD . 若 , , 则( ) A、24° B、24.5° C、25° D、25.5°9. 下列说法中,正确的有( )个
A、24° B、24.5° C、25° D、25.5°9. 下列说法中,正确的有( )个①两个全等的三角形一定关于某直线对称;
②关于某条直线对称的两个图形,对称点所连线段被对称轴垂直平分;
③等腰三角形的高、中线、角平分线互相组合;
④到三角形三个顶点距离相等的点是这个三角形三边垂直平分线的交点;
⑤的三边为a,b,c,且满足关系 , 则为等边三角形.
A、1个 B、2个 C、3个 D、4个10. 已知:是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边的内部时,那么和的数量关系是( )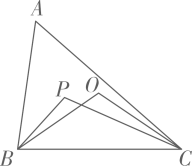 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M、N . 作直线MN , 交AC于点D , 交BC于点E , 连接BD . 若AB=7,AC=12,BC=6,则△ABD的周长为 .
 12. 如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB , BC于点D、E , AC的垂直平分线分别交AC , BC于点F、G , 则△AEG的周长为 .
12. 如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB , BC于点D、E , AC的垂直平分线分别交AC , BC于点F、G , 则△AEG的周长为 .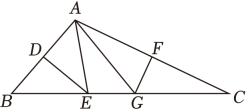 13. 如图,直线l1、l2分别垂直平分线段AB、BC交于点O,直线l1交BC于点E.若∠AOC=72°,则∠DOE=°.
13. 如图,直线l1、l2分别垂直平分线段AB、BC交于点O,直线l1交BC于点E.若∠AOC=72°,则∠DOE=°. 14. 如图,在△ABC中,∠BAC=120°,点D是BC上一点,BD的垂直平分线交AB于点E , 将△ACD沿AD折叠,点C恰好与点E重合,则∠B等于°.
14. 如图,在△ABC中,∠BAC=120°,点D是BC上一点,BD的垂直平分线交AB于点E , 将△ACD沿AD折叠,点C恰好与点E重合,则∠B等于°. 15. 如图,在等腰中, , 点M,N分别是边 , 上的动点,与关于直线对称,点B的对称点为 . 当且时,若 , 则的面积为.
15. 如图,在等腰中, , 点M,N分别是边 , 上的动点,与关于直线对称,点B的对称点为 . 当且时,若 , 则的面积为.
三、作图题
-
16. 在如图所示的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点的坐标分别为A(-3,3),B(-1,1),C(-5,-3).
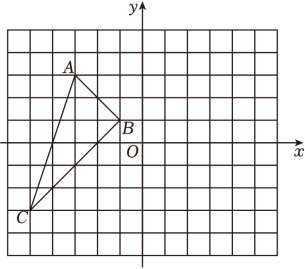
画出△ABC关于y轴成轴对称的△A1B1C1 , 并写出点A1的坐标;
请直接写出△A1B1C1的面积;
在y轴上找一点P , 使PA=PB , 并写出点P的坐标.
四、解答题
-
17. 在等边△ABC中,点D是边BC上一点.作射线AD , 点B关于射线AD的对称点为点E . 连接CE并延长,交射线AD于点F .
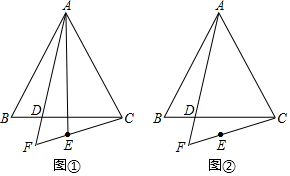 (1)、如图①,连接AE ,
(1)、如图①,连接AE ,①AE与AC的数量关系是 ▲ ;
②设∠BAF=a , 用a表示∠BCF的大小;
(2)、如图②,用等式表示线段AF , CF , EF之间的数量关系,并证明.18. 如图,在中, , 的垂直平分线交于点 , 交于点. (1)、若 , 则的度数是;若 , 则的度数是;(2)、你认为与有怎样的数量关系?请说明理由;(3)、连接 , 若 , 的周长是16cm,求的长;(4)、点是边上的中点,连接 , 与直线相交于点 , 点到三个顶点的距离有怎样的关系?请说明理由.19. 在中为直角, , 为外一点,且 , 交延长线于点 , 探求 , , 之间有何数量关系.
(1)、若 , 则的度数是;若 , 则的度数是;(2)、你认为与有怎样的数量关系?请说明理由;(3)、连接 , 若 , 的周长是16cm,求的长;(4)、点是边上的中点,连接 , 与直线相交于点 , 点到三个顶点的距离有怎样的关系?请说明理由.19. 在中为直角, , 为外一点,且 , 交延长线于点 , 探求 , , 之间有何数量关系. 20. 已知△ACD中,AC=AD,∠CAD=α,∠PAC=30°,将点C关于直线AP对称,得到点B,连接BA.
20. 已知△ACD中,AC=AD,∠CAD=α,∠PAC=30°,将点C关于直线AP对称,得到点B,连接BA.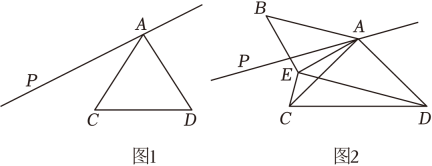 (1)、连接BD,
(1)、连接BD,①依题意,在图1中补全图形;
②若α=80°,则∠BDC的度数为 ▲ ;
③当α的度数发生变化时,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数 ;若改变,请说明理由.
(2)、如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD, 连接CE,DE.若α=90°.求证:CE⊥ED.21. 如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处, (1)、求∠ECF的度数;(2)、若CE=4,B′F=1,求线段BC的长和△ABC的面积.
(1)、求∠ECF的度数;(2)、若CE=4,B′F=1,求线段BC的长和△ABC的面积.
-