人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——第十二章综合测试

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列命题是真命题的是（）

A、形状相同的两个三角形全等 B、三边分别相等的两个三角形全等 C、周长相等的两个三角形全等 D、两边分别相等且其中一组等边的对角相等的两个三角形全等

查看试题解析
2. 如图， $A M$ 垂直 $∠ A B C$ 的平分线 $B M$ 于点 $M$ ， $D$ 为 $B C$ 中点，连接 $M D$ ，若 $△ A B C$ 的面积为4，则 $△ B M D$ 的面积为（）

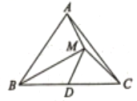A、1 B、2 C、2.5 D、3

查看试题解析
3. 已知，如图所示，AD＝AC ， BD＝BC ， O为AB上一点，那么，图中共有（　　）对全等三角形

A、1 B、2 C、3 D、4

查看试题解析
4. 如图是用直尺和圆规作已知角∠AOB平分线OP的示意图，仔细观察，根据三角形全等的知识，说明画出OP的依据是（　　）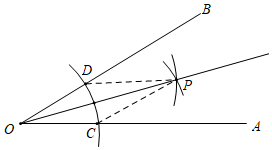

A、边角边，全等三角形对应角相等 B、角边角，全等三角形对应角相等 C、边边边，全等三角形对应角相等 D、斜边直角边，全等三角形对应角相等

查看试题解析
5. 如图，在Rt△ABC中，AC＝6，BC＝8，AB＝10．点P从点A出发，以每秒2个单位长度的速度沿折线A-C-B向终点B运动，同时点Q从点B出发，以每秒3个单位长度的速度沿折线B-C-A向终点A运动，点P ， Q都运动到各自的终点时停止．设运动时间为t（秒），直线l经过点C ，且l∥AB ，过点P ， Q分别作直线l的垂线段，垂足为E ， F ．当△CPE与△CQF全等时，t的值不可能是（　　）

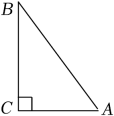A、2 B、2.8 C、3 D、6

查看试题解析
6. 如图 $∠ A C B = 90 °$ ， $A C = B C$ ， $A D ⊥ C E$ ， $B E ⊥ C E$ ，垂足分别是点D ， E ，若 $A D = 3$ ， $B E = 1$ ，则 $D E$ 的长是（　　）

A、2 B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
7. 如图，在△ABC中，BE平分∠ABC，DE垂直平分AB，下列说法不一定正确的是（）

A、AE＝BE B、∠AED+∠EBC＝90° C、∠DAE＝∠EBC D、∠BAE＝∠CAE

查看试题解析
8. 如图，在△ABC中，CD⊥AB于点D，EF⊥AC交CD于点E，连接AE，若ED＝EF，∠ECF＝58°，则∠DAE＝（）

A、32° B、18° C、16° D、29°

查看试题解析
9. 如图，点 $A ， E ， F ， C$ 在同一直线上， $B F ⊥ A C$ 于点 $F ， D E ⊥ A C$ 于点 $E$ ，连结 $B D$ ，交 $E F$ 于点 $O$ ，且 $O$ 为 $E F$ 的中点．若 $A E = C F$ ，则下列结论：① $△ E O D ≌ △ F O B$ ；② $A O = C O$ ；③ $A B = C D$ ；④ $A B / / C D$ ，其中正确的是（）

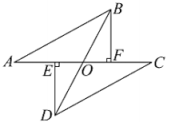A、①② B、③④ C、①②③ D、①②③④

查看试题解析
10. 如图， $B D$ 平分 $∠ A B C$ ， $F$ ， $G$ 分别是 $B A$ ， $B C$ 上的点 $(B F \neq B G)$ ， $E F = E G$ ，则 $∠ B F E$ 与 $∠ B G E$ 的数量关系一定满足的是（）

A、 $∠ B F E + ∠ B G E = 90 °$ B、 $∠ B F E + ∠ B G E = 180 °$ C、 $∠ B F E = 2 ∠ B G E$ D、 $∠ B F E - ∠ B G E = 90 °$

查看试题解析

二、填空题

11. 如图，∠ACD＝∠BCE，BC＝EC，要使△ABC≌△DEC，则可以添加的一个条件是．

查看试题解析
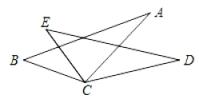12. 如图，AE与BD相交于点C ， $A C = E C$ ， $B C = D C$ ， $A B = 8 c m$ ，点P从点A出发，沿A→B→A方向以3cm/s的速度运动，点Q从点D出发，沿D→E方向以1 cm/s的速度运动，P、Q两点同时出发.当点P到达点A时，P、Q两点同时停止运动.设点P的运动时间为 $t (s)$ .连接PQ，当线段PQ经过点C时，t的值为s.

查看试题解析
13. 如图，点E、A、C在同一条直线上，AB∥CD，AB=CE，AC=CD，若∠D=40°，∠ECD=115°，则∠B=度．

查看试题解析
14. 如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，若∠A =∠ABE，AC = 10，BC = 6，则BD的长为

查看试题解析
15. 如图， $△ A B C$ 中， $∠ A B C$ 、 $∠ F C A$ 的角平分线 $B P$ 、 $C P$ 交于点 $P$ ，延长 $B A$ 、 $B C$ ， $P M ⊥ B E$ 于 $M$ ， $P N ⊥ B F$ 于 $N$ ，则下列结论：① $A P$ 平分 $∠ E A C$ ；② $∠ A B C + 2 ∠ A P C = 180 °$ ；③ $∠ B A C = 2 ∠ B P C$ ；④ $S_{△ P A C} = S_{△ M A P} + S_{△ N C P}$ ．其中正确结论序号是．

查看试题解析

三、解答题

16. 如图，在等边△ABC中，D，E分别是BC，AC上的点，且AE=CD．AD与BE交于点N，BM⊥AD于点M．
求证：

(1)、△ABE≌△CAD；

(2)、MN= $\frac{1}{2}$ BN．

查看试题解析
17. 如图，P为等边△ABC内一点，连接BP、PC，延长PC到点D，使CD= PC；延长BC到点E，使CE=BC，连接AE、DE．

(1)、求证：BP∥DE；

(2)、求∠BAE的度数；

(3)、若BP⊥AC，则∠AED=度．

查看试题解析
18. 如图，△ABC中，D为BC上一点，∠ADC＝60°，AE⊥BC于点E ， CF⊥AD于点F ， AE、CF相交于点G ， ∠CAE＝15°．

(1)、求∠ACF的度数；

(2)、求证： $D F = \frac{1}{2} A G$ ．

查看试题解析
19. 如图①，在△ABC中，∠ACB=90°，AC=BC，点P是线段AB上的一点，过点A作AE⊥CP，交CP的延长线于点E，过点B作BF⊥CP于点F．

(1)、若BF=8，AE=3，则EF=

(2)、在图①中，线段AE、BF、EF有怎样的数量关系？请说明理由；

(3)、如图②，在△ABC中，∠ACB=90°，AC=BC，点P是△ABC内部的一点，且BP⊥CP，连接AP，若CP=5，求△ACP的面积．

查看试题解析
20. 如图，△ABC中，∠ACB=90°，DC=AE，AE是BC边上的中线，过点C作CF⊥AE，垂足为点F，过点B作BD⊥BC交CF的延长线于点D．

(1)、求证：AC=CB．

(2)、若AC=12cm，求BD的长．

查看试题解析
21.
如图，在 $△ A B D$ 中， $∠ A B C = 45 °$ ， $A C$ ， $B F$ 为 $△ A B D$ 的两条高．

(1)、求证： $B E = A D$ ；

(2)、若过点 $C$ 作 $C M / / A B$ ，交 $A D$ 于点 $M$ ，求证： $B E = A M + E M$ ．

查看试题解析
22. 如图，在 $△ A B C$ 中，ADBC于点D ，点E在AD上， $D E = D C$ ， $B E = A C$ ，点F为BC的中点，连接EF并延长至点M ，使 $F M = E F$ ，连接CM ．求证：

(1)、 $△ B D E ≌ △ A D C$ ；

(2)、 $A C ⊥ M C$ ．

查看试题解析
23. 将两个全等的 $R t △ A B C$ 和 $R t △ D B E$ 按图1方式摆放，其中 $∠ A C B = ∠ D E B = 90 °$ ，点E落在 $A B$ 上， $D E$ 所在直线交直线 $A C$ 于点F ．

(1)、求证： $C F = E F$ ；

(2)、若将图1中 $△ D B E$ 绕点B按顺时针方向旋转到图2位置，其他条件不变（如图2），请写出此时 $A F$ 、 $E F$ 与 $D E$ 之间的数量关系，并加以证明．

查看试题解析