人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——12.3角平分线的性质

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列说法中正确的个数是（）
$(1) 三角形具有稳定性$
$(2)$ 到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点
$(3)$ 在角的内部到角两边距离相等的点在角的平分线上；
$(4)$ 有两边和其中一边的对角分别相等的两个三角形不一定全等；
$(5)$ 等腰三角形的角平分线，中线，高线互相重合，简称三线合一．

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
2. 如图，在Rt△ABC中，∠ACB＝90°，AD平分∠CAB，若CD＝10，则点D到AB的距离是（　　）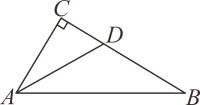

A、8 B、9 C、10 D、11

查看试题解析
3. 如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF，给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AB＝3BF；⑤S_△_ADB＝2S_△_BDF ，其中正确的结论共有（）

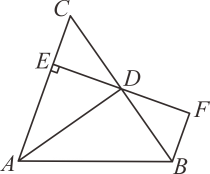A、5个 B、4个 C、3个 D、2个

查看试题解析
4. 如图：∠DAE＝∠ADE＝15°，DE∥AB ， DF⊥AB ，若AE＝8，则DF等于（　　）

A、10 B、7 C、5 D、4

查看试题解析
5. 如图，在△ABC中，AB＝3，AC＝4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N，则△AMN的周长为（）

A、4 B、6 C、7 D、8

查看试题解析
6. 如图， $△ A B C$ 中， $A B = A C$ ， AD平分 $∠ B A C$ ， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别是E、F，则下列四个结论中：①AD上任意一点到B、C的距离相等；②AD任意一点到AB、AC的距离相等；③ $A D ⊥ B C$ 且 $B D = C D$ ；④ $∠ B D E = ∠ C D F$ ．其中正确的是（）

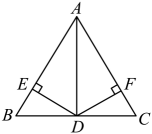A、①④ B、②④ C、②③④ D、①②③④

查看试题解析
7. 如图， $∠ A O B = 30 °$ ， OP平分 $∠ A O B$ ， $P C ∥ O B$ ， $P D ⊥ O B$ ，若 $P C = 4$ ，则 $P D =$ （）

A、2 B、4 C、6 D、8

查看试题解析
8. 如图， $A E$ ， $B E$ ， $C E$ 分别平分 $∠ B A C$ ， $∠ A B C$ ， $∠ A C B$ ， $E D ⊥ B C$ 于点 $D$ ， $E D = 1$ ， $△ A B C$ 的面积为 $12$ ，则 $△ A B C$ 的周长为（）

A、 $4$ B、 $6$ C、 $24$ D、 $12$

查看试题解析
9. 若三角形内一点到三角形三条边的距离相等，则这点一定是三角形（）

A、三边垂直平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条内角平分线的交点

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A B C = 3 ∠ C$ ， $A D$ 为 $∠ B A C$ 的平分线， $B M ⊥ A D$ ，垂足为M，且 $A B = 6$ ， $B M = 2$ ，则 $A C =$ （）．

A、10 B、7 C、8 D、9

查看试题解析

二、填空题

11. 如图，在Rt△BC中，∠C=90°。以顶点B为圆心、BC长为半径作圆弧，交AB于点D，再分别以点C和点D为圆心、大于 $\frac{1}{2}$ CD长为半径作圆弧，两弧交于点E．作射线BE交AC于点F．若BC=12，AB=15，△BCF的面积为24．则△ABC的面积为

查看试题解析
12. 如图，在△ABC中，∠ACB＝90°，AC＝BC ， D为AB的中点，点M、N分别在AC、CB的延长线上，且MD⊥DN ，连MN ．若∠DMC＝15°，BN＝1，则MN的长是．

查看试题解析
13. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补．若∠MPN在绕点P旋转的过程中，其两边分别与OA，OB相交于M、N两点，则以下结论：①PM＝PN恒成立，②OM＋ON的值不变，③四边形PMON的面积不变，④MN的长不变，其中正确的为（请填写结论前面的序号）．

查看试题解析
14. 如图，△ABC中∠A＝60°，点M，N分别是∠ABC与∠ACB三等分线的交点，则∠BMN的度数是 °．

查看试题解析
15. 如图，在 $△ A B C$ 中，内角 $∠ B A C$ 与外角 $∠ C B E$ 的平分线相交于点P， $B E = B C$ ， $P B$ 与 $C E$ 交于点H， $P G ∥ A D$ 交 $B C$ 于点F，交 $A B$ 于点G，连接 $C P$ ．
下列结论：① $∠ A C B = 2 ∠ A P B$ ；② $S_{△ P A C} ： S_{△ P A B} = A C ： A B$ ；③ $B P$ 垂直平分 $C E$ ；④ $∠ P C F = ∠ C P F$ ．其中，正确的结论有．（填序号）

查看试题解析

三、解答题

16. 如图，已知∠A=∠D=90°，点E，F在线段BC上，DE与AF交于点O，且AB=DC，BE=CF．

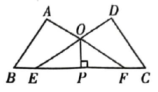(1)、求证：AF=DE；

(2)、若OP⊥EF，求证：OP平分∠EOF．

查看试题解析
17. 如图，在△ABC中，AD是高线，AE、BF是角平分线，它们相交于点O ， ∠BAC＝50°，∠C＝70°，求∠EAD与∠BOA的度数．

查看试题解析
18. 如图，AB∥CD ， M是AD的中点，BM⊥CM ，连接BC ．

(1)、求证：CM平分∠BCD；

(2)、探究BC、CD、AB之间的数量关系．

查看试题解析
19. 如图，CB=CD，∠D+∠ABC=180°，CE⊥AD于E，CF⊥AB交AB的延长线于点F．

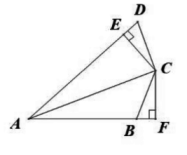(1)、求证：AC平分∠DAB；

(2)、若AE=8，DE=2，求AB的长．

查看试题解析
20. 如图，在△ABC中，BD，CE分别是∠ABC，∠ACB的平分线．

(1)、若∠ABC=60°，∠ACB=40°，求∠BPC的度数．

(2)、若∠A=80°，求∠BPC的度数．

(3)、若∠A=x度，用含x的代数式表示∠BPC的度数．

查看试题解析
21. 如图，在四边形ABDC中，∠D=∠B=90°，O为BD的中点，且AO平分∠BAC．
求证：

(1)、CO平分∠ACD．

(2)、AB+CD=AC．

查看试题解析
22. 如图，在 $△ A O B$ 和 $△ C O D$ 中， $O A = O B$ ， $O C = O D$ ， $O A < O C$ ， $∠ A O B = ∠ C O D = 36 °$ ．
连接 $A C$ ， $B D$ 交于点 $M$ ，连接 $O M$ ．
（Ⅰ）求证： $A C = B D$ ；
（Ⅱ）求 $∠ A M B$ 的大小；
（Ⅲ）求证： $∠ A M O = ∠ D M O$

查看试题解析
23. 小聪和小明两位同学在学习全等三角形时积极思考，提出了以下两个问题：
问题 $1$ ：如图 $1$ ， $△ A B C$ 中， $A B = 3$ ， $A C = 2$ ， $A D$ 是 $△ A B C$ 的角平分线，求 $B D$ ： $D C$ 的值．
小聪同学经过思考，发现可以过 $D$ 作 $D M ⊥ A B$ 于 $M$ ， $D N ⊥ A C$ 于 $N$ ，利用 $△ A B D$ 与 $△ A C D$ 的面积比来解决这个问题．
问题 $2$ ：如图 $2$ ， $△ A B C$ 为等边三角形，点 $D$ 为 $△ A B C$ 外一点， $∠ C D A = 60 °$ ，连接 $D B$ ，探究 $A D$ ， $C D$ ， $B D$ 三者之间的数量关系．
小明同学经过思考，发现可以在 $D A$ 上截取 $D E = D C$ ，构造等边三角形 $C D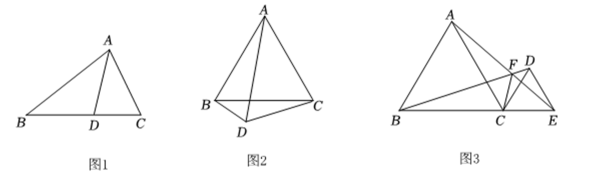 E$ ，从而解决这个问题．

(1)、根据两位同学的思考，完成问题 $1$ 、 $2$ 的解答 $($ 直接写出结果 $)$ ．

(2)、根据问题 $1$ 、 $2$ 的结论，解决下面问题：如图 $3$ ， $△ A B C$ 和 $△ C D E$ 都是等边三角形，且 $B$ 、 $C$ 、 $E$ 三点共线，连接 $A E$ ， $B D$ 交于点 $F$ ，连接 $F C$ ，设 $A F = a$ ， $D F = b$ ， $C F = c$ ，若 $B C = 2 C E$ ，直接写出 $\frac{a - 2 b}{3 c}$ 的值．

查看试题解析