【北师大版】2023-2024学年数学七年级(上)期末仿真模拟试题(一)
试卷更新日期:2023-12-12 类型:期末考试
一、选择题
-
1. 如图是几何体的俯视图,所表示数字为该位置小正方体的个数,则该几何体的正视图是( )
 A、
A、 B、
B、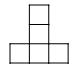 C、
C、 D、
D、 2. 用计算器计算230 , 按键顺序正确的是( )A、2 3 0= B、2×3 0= C、2 3 0 xm= D、2 xm 3 0=3. 如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )
2. 用计算器计算230 , 按键顺序正确的是( )A、2 3 0= B、2×3 0= C、2 3 0 xm= D、2 xm 3 0=3. 如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )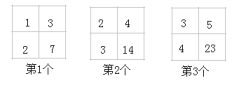 A、62 B、79 C、88 D、984. 下列说法中,正确的是( )A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧5. 一列长150米的火车,以每秒15米的速度通过长600米的桥洞,从列车进入桥洞口算起,这列火车完全通过桥洞所需时间是( )A、40秒 B、60秒 C、50秒 D、34秒6. 为了反映今天的气温变化情况,你认为选择哪种统计图最恰当( )A、频数直方图 B、条形统计图 C、扇形统计图 D、折线统计图7. 如图,D,E顺次为线段AB上的两点,AB=20,C为AD的中点,则下列选项中正确的是( )
A、62 B、79 C、88 D、984. 下列说法中,正确的是( )A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧5. 一列长150米的火车,以每秒15米的速度通过长600米的桥洞,从列车进入桥洞口算起,这列火车完全通过桥洞所需时间是( )A、40秒 B、60秒 C、50秒 D、34秒6. 为了反映今天的气温变化情况,你认为选择哪种统计图最恰当( )A、频数直方图 B、条形统计图 C、扇形统计图 D、折线统计图7. 如图,D,E顺次为线段AB上的两点,AB=20,C为AD的中点,则下列选项中正确的是( ) A、若BE-DE=0,则AE-CD= 7 B、若BE-DE=2,则AE-CD=7 C、若BE-DE=4,则AE-CD=7 D、若BE-DE=6,则AE-CD=78. 图1是由3个相同小长方形拼成的图形其周长为24 , 图2中的长方形内放置10个相同的小长方形,则长方形的周长为( )
A、若BE-DE=0,则AE-CD= 7 B、若BE-DE=2,则AE-CD=7 C、若BE-DE=4,则AE-CD=7 D、若BE-DE=6,则AE-CD=78. 图1是由3个相同小长方形拼成的图形其周长为24 , 图2中的长方形内放置10个相同的小长方形,则长方形的周长为( ) A、 B、 C、 D、9. 右图是“大润发”超市中“飘柔”洗发水的价格标签,一服务员不小心将墨水滴在标签上,使得原价看不清楚,该洗发水的原价为( )
A、 B、 C、 D、9. 右图是“大润发”超市中“飘柔”洗发水的价格标签,一服务员不小心将墨水滴在标签上,使得原价看不清楚,该洗发水的原价为( ) A、22元 B、23元 C、24元 D、26元10. 如图,在同一平面内, , , 点为反向延长线上一点(图中所有角均指小于的角).下列结论:①;②;③;④.其中正确结论的个数有( ).
A、22元 B、23元 C、24元 D、26元10. 如图,在同一平面内, , , 点为反向延长线上一点(图中所有角均指小于的角).下列结论:①;②;③;④.其中正确结论的个数有( ).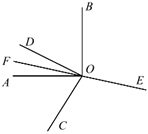 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 韩城市为了能源结构优化、生态环境保护,以及推动绿色低碳高质量发展,计划投产大唐西庄农光互补光伏发电项目,总投资470000000元.将数据470000000用科学记数法表示为.12. 已知 , , 则.13. 已知关于x的方程与的解相同,则.14. 对我国“天宫空间站梦天实验舱”的零部件检查应采用的调查方式为.(填“普查”或“抽样调查”).15. 从八边形的一个顶点引出的对角线有条.
三、解答题
-
16. 如图所示:已知在数轴上的位置
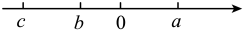 (1)、化简:(2)、若a的绝对值的相反数是的倒数是它本身, , 求的值.17. 如图是一个正方体的表面展开图,它的每一个面上都写有一个数,并且相对的两个面的数字互为相反数,求的值.
(1)、化简:(2)、若a的绝对值的相反数是的倒数是它本身, , 求的值.17. 如图是一个正方体的表面展开图,它的每一个面上都写有一个数,并且相对的两个面的数字互为相反数,求的值.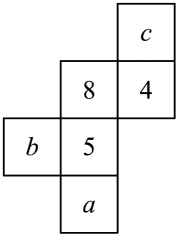 18. 初中一年级就“喜欢的球类运动”曾进行过问卷调查,每人只能报一项,结果300人回答的情况如下表,请用扇形统计图表示出来,根据图示的信息再制成条形统计图。
18. 初中一年级就“喜欢的球类运动”曾进行过问卷调查,每人只能报一项,结果300人回答的情况如下表,请用扇形统计图表示出来,根据图示的信息再制成条形统计图。排球
25
篮球
50
乒乓球
75
足球
100
其他
50
 19. 如图,平面上有A,B,C,D四点,请用直尺和圆规作图(不要求写作图过程).
19. 如图,平面上有A,B,C,D四点,请用直尺和圆规作图(不要求写作图过程).( 1 )作直线AD、线段BC.
( 2 )在射线AD上作AP=2AB- BC.
( 3 )找一点O,使它到A,B,C,D四点的距离之和最小.
 20. 在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A:国学诵读”、“B:演讲”、“C:课本剧”、“D:书法”.要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示:
20. 在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A:国学诵读”、“B:演讲”、“C:课本剧”、“D:书法”.要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示: (1)、被调查的总人数为人;扇形统计图中,活动A所占圆心角为度;活动D所占圆心角为度.(2)、请补全条形统计图:学校共有1600名学生,试估算希望参加活动A的学生有多少人?21. [阅读理解]
(1)、被调查的总人数为人;扇形统计图中,活动A所占圆心角为度;活动D所占圆心角为度.(2)、请补全条形统计图:学校共有1600名学生,试估算希望参加活动A的学生有多少人?21. [阅读理解]射线OC是∠AOB内部的一条射线,若∠COA=∠AOB,则我们称射线OC是射线OA的“友好线”.例如,图1中,AOB=60°,∠AOC= ZCOD=∠BOD= 20°,则∠AOC=∠AOB,称射线OC是射线OA的“友好线”;同时,由于∠BOD=∠AOB,称射线OD是射线OB的“友好线”

[知识运用]
(1)、如图2,∠AOB=120°,射线OM是射线OA的“友好线”,则∠AOM=(2)、如图3,∠AOB=180°,射线OC与射线OA重合,并绕点O以每秒2°的速度逆时针旋转,射线OD与射线OB重合,并绕点O以每秒3°的速度顺时针旋转,当射线OD与射线OA重合时,运动停止.①是否存在某个时刻t(秒),使得∠COD的度数是40° ,若存在,求出t的值,若不存在,请说明理由..
②当t为多少秒时,射线OC,OD,OA中恰好有一条射线是另一条射线的“友好线”。(直接写出答案)
22. 某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:用水量/月
单价(元/)
不超过
超过的部分
另:每立方米用水加收元的城市污水处理费和元的城市附加费
(1)、根据上表,用水量每月不超过 , 实际每立方米收水费多少元?如果10月份某用户用水量为 , 那么该用户10月份应该缴纳水费多少元?(2)、某用户11月份共缴纳水费80元,那么该用户11月份用水多少?(3)、若该用户水表12月份出了故障,有25%的水量没有计入水表中,这样该用户在12月份只缴纳了54元水费,问该用户12月份实际应该缴纳水费多少元?