人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——12.2全等三角形的判定

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同的刻度分别与点M ， N正合，过角尺顶点C连OC ．可知△OMC≌△ONC ， OC便是∠AOB的平分线．则△OMC≌△ONC的理由是（）

A、SSS B、SAS C、AAS D、HL

查看试题解析
2. 如图，∠A=∠D，∠1=∠2，要使△ABC≌△DEF，还应给出的条件是（）

A、∠E=∠B B、ED=BC C、AB=EF D、AF=CD

查看试题解析
3. 下列命题是假命题的是（）

A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两边分别相等且其中一组等边的对角相等的两个三角形全等 D、两角分别相等且其中一组等角的对边相等的两个三角形全等

查看试题解析
4. 如图，∠C＝90°，AD平分∠BAC，DE⊥AB于点E，有下列结论：①CD＝ED；②AC+BE＝AB；③DA平分∠CDE；④∠BDE＝∠BAC；⑤S_△ABD：S_△ACD＝AB：AC．其中结论正确的个数有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 如图，把一长一短两根细木棍的一端用螺钉铰合在一起，使长木棍的另一端与射线BC的端点B重合，固定住长木棍，摆动短木棍，使端点分别落在射线BC上的C、D两位置时，形成了 $△ A B D$ 和 $△ A B C$ ．此时 $A B = A B ， A C = A D ， ∠ A B D = ∠ A B C$ ，但是 $△ A B D$ 和 $△ A B C$ 不全等，这说明（）

A、三角对应相等的两个三角形不一定全等 B、两边及一边对角对应相等的两个三角形不一定全等 C、两角及一角对边对应相等的两个三角形不一定全等 D、两边及夹角对应相等的两个三角形不一定全等

查看试题解析
6. 如图， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E$ ，点 $B$ ， $D$ ， $E$ 在同一直线上，若 $∠ 1 = 25 °$ ， $∠ 2 = 35 °$ ，则 $∠ 3$ 的度数是（）

A、50° B、55° C、60° D、70°

查看试题解析
7. 如图，已知 $△ A B C$ 和 $△ D C E$ 均是等边三角形，点B、C、E在同一条直线上， $A E$ 与 $B D$ 交于点O， $A E$ 与 $C D$ 交于点G， $A C$ 与 $B D$ 交于点F，连接 $O C 、 F G$ ，则下列结论：① $A E = B D$ ；② $A G = B F$ ；③ $∠ B O E = 120 °$ ．其中结论正确的（）

A、①②③ B、①③ C、②③ D、①

查看试题解析
8. 如图，在△ABC和△ADE中，∠CAB＝∠DAE＝36°，AB＝AC，AD＝AE.连接CD，连接BE并延长交AC，AD于点F，G.若BE恰好平分∠ABC，则下列结论错误的是（）

A、∠ADC＝∠AEB B、 $C D ∥ A B$ C、DE＝GE D、CD＝BE

查看试题解析
9. 如图，△ABC中，AB＝AC ， ∠BAC=90°，点D在线段BC上， $∠ E D B = \frac{1}{2} ∠ A C B$ ， BE⊥DE ， DE与AB相交于点F，若BE＝3，则DF＝（　　）

A、7 B、 $\frac{13}{2}$ C、6 D、 $\frac{11}{2}$

查看试题解析
10. 如图所示，在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：
①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有①，②，③，④的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块．

查看试题解析
12. 如图，在 $△ A D E$ 中， $A G ⊥ D E$ 于点 $G$ ， $F$ 是 $D E$ 上一点， $B$ 是 $△ A D E$ 外一点，且 $A B = A D$ ，连接 $B F$ ， $C$ 是 $B F$ 上的一点， $A C = A E$ ， $∠ B A D = ∠ C A E$ ， $S_{△ A D E} = 30$ ， $A G = 5$ ， $C F = 2$ ，则 $B F$ 的长为.

查看试题解析
13. 如图，已知 $∠ A C B = 90 °$ ， $A C = B C$ ， $A D ⊥ C E$ ， $B E ⊥ C E$ ，垂足点分别是 $D$ ， $E$ ， $A D = 5$ ， $B E = 2$ ，则 $D E$ 的长为．

查看试题解析
14. 如图，有一个 $R t △ A B C$ ， $∠ C = 90 °$ ， $A C = 16$ ， $B C = 8$ ，一条线段 $M N = A B$ ， $M$ ， $N$ 分别在 $A C$ 和过 $A$ 点且垂直于 $A C$ 的射线 $A P$ 上运动， $A M =$ 时，才能使 $△ A B C$ 与 $△ A M N$ 全等．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A B C = 45 °$ ， $C D ⊥ A B$ 于点D ， BE平分 $∠ A B C$ ，且 $B E ⊥ A C$ 于点E ，与CD相交于点F ， $D H ⊥ B C$ 于点H ，交BE于点G ．下列结论：
① $B D = C D$ ；② $A D + C F = B D$ ；③ $C E = \frac{1}{2} B F$ ；④ $A E = C F$ ．
其中正确的是．

查看试题解析

三、解答题

16. 在等边△ABC中，点D是边BC上一点．作射线AD ，点B关于射线AD的对称点为点E ．连接CE并延长，交射线AD于点F ．

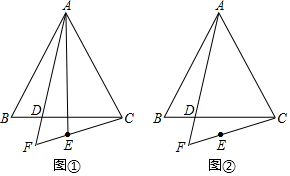(1)、如图①，连接AE ，
①AE与AC的数量关系是 ▲ ；
②设∠BAF＝a ，用a表示∠BCF的大小；

(2)、如图②，用等式表示线段AF ， CF ， EF之间的数量关系，并证明．

查看试题解析
17. 如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE ， ∠1＝∠2，求证：Rt△ADE≌Rt△BEC ．

查看试题解析
18. 已知：如图，AB∥CD，AD交BC于点O，EF过点O，分别交AB，CD于点E，F，且AE=DF．求证：O是EF的中点．

查看试题解析
19. 如图，在 $△ A B C$ 中，D是 $B C$ 的中点，过点D的直线 $G F$ 交 $A C$ 于点F ，交 $A C$ 的平行线 $B G$ 于点G ， $D E ⊥ G F$ 交 $A B$ 于点E ，连接 $E G ， E F$ ．

(1)、求证： $△ B D G ≌ △ C D F$ ；

(2)、请你判断 $B E + C F$ 与 $E F$ 的大小关系，并说明理由．

查看试题解析
20. 在 $△ A B C$ 中， $A B = A C$ ，点D是直线BC上的一点（不与B、C重合），以AD为一边在AD的右侧做 $△ A D E$ ，使 $A D = A E ， ∠ D A E = ∠ B A C$ ，连接CE

(1)、如图1，点D在线段BC上，若 $∠ B A C = 90 °$ ，求 $∠ D C E$ 的度数：设 $∠ B A C = α ， ∠ B C E = β$ ；

(2)、如图2，若点D在线段BC上移动，则 $α$ 和 $β$ 有怎样的数量关系，并说明理由；

(3)、若点D在直线BC上移动，则 $α$ 和 $β$ 有怎样的数量关系，请直接写出结论．

查看试题解析
21. 如图，已知 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 ° .$ 分别过 $A$ 、 $B$ 向过点 $C$ 的直线作垂线，垂足分别为点 $M$ 、 $N$ ．

(1)、如图 $1$ ，过 $C$ 的直线与斜边 $A B$ 不相交时，求证： $M N = A M + B N$ ．

(2)、如图 $2$ ，过 $C$ 的直线与斜边 $A B$ 相交时，其他条件不变，若 $A M = 10$ ， $B N = 3$ ，试求 $M N$ 的长．

查看试题解析
22. 问题背景：

(1)、如图1：在四边形ABCD中，AB＝AD ， ∠BAD＝120°，∠B＝∠ADC＝90°．E ， F分别是BC ， CD上的点．且∠EAF＝60°．探究图中线段BE ， EF ， FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G ．使DG＝BE ．连接AG ，先证明△ABE≌△ADG ，再证明△AEF≌△AGF ，可得出结论，他的结论应是．
探索延伸：

(2)、如图2，若在四边形ABCD中，AB＝AD ， ∠B+∠D＝180°．E ， F分别是BC ， CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠BAD ，上述结论是否仍然成立，并说明理由．

查看试题解析
23. 阅读下面材料：小明遇到这样一个问题：如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线， $E$ 是 $A D$ 上一点，延长 $B E$ 交 $A C$ 于点 $F$ ， $A F = E F$ ，求证： $A C = B E$ ．
小明发现，延长AD到点H，使DH=AD，连结BH，构造 $△ B D H$ ，通过证明 $△ B D H$ 与 $△ A C D$ 全等， $△ B E H$ 为等腰三角形，使问题得以解决（如图2）．请写出推导过程．

查看试题解析