山东省济南市莱芜区2023-2024学年七年级上学期中考试数学试卷（五四学制）
试卷更新日期：2023-12-12 类型：期中考试
一、选择题（每小题的四个选项中，只有一个是正确的，请把正确答案的字母代号选出来）
-
1. 下列图案或文字中，是轴对称图形的有（ ）
A、2个 B、3个 C、4个 D、5个2. 下列说法正确的是（ ）A、的平方根是±4 B、-表示6的算术平方根的相反数 C、任何数都有平方根 D、-a2一定没有平方根3. 下列各数中是无理数的有（ ）， π，-3， ， -3.1416， ， 0.2121121112...（相邻两个2之间1的个数逐次加1）
A、2个 B、3个 C、4个 D、5个4. 如果一个等腰三角形的周长为15cm，一边长为3cm，那么腰长为（ ）A、3cm B、6cm C、5cm D、3cm或6cm5.如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）
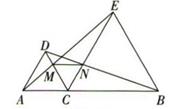
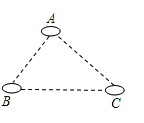A、在AC，BC两边高线的交点处 B、在AC，BC两边中线的交点处 C、在AC，BC两边垂直平分线的交点处 D、在两内角平分线的交点处6. 如图，已知∠1＝∠2，AC＝AD ， 增加下列条件：①AB＝AE；②BC＝ED；③∠C＝∠D；④∠B＝∠E ． 其中能使△ABC≌△AED成立的条件有（ ）
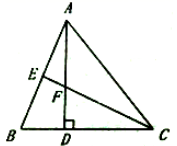
A、4个 B、3个 C、2个 D、1个7. 若等腰三角形腰上的高是腰长的一半，则这个等腰三角形的底角是（ ）A、75°或15° B、75° C、15° D、75°和30°8. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（ ）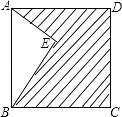
A、48 B、60 C、76 D、809. 如图，△ABC中，AD⊥BC ， 垂足为D ， BE⊥AC ， 垂足为E ， AD、BE相交于点F ． 如果BF＝AC ， 那么∠ABC的度数是（ ）
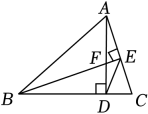A、40° B、45° C、50° D、60°10. 如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于（ ）
A、50° B、75° C、80° D、105°二、填空题
-
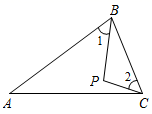
11. 如果与（2x-4）2互为相反数，那么2x-y＝ ．12. 如图，点P是△ABC内一点，∠ABC=80°，∠1=∠2，则∠BPC=度．
13. 如图，在△ABC中，DE是AC的垂直平分线，△ABC的周长为19cm ， △ABD的周长为13cm ， 则AE的长为 ．
14. 如图，圆柱形玻璃杯，底面周长为16cm ， AC是底面圆的直径，点P是BC上的一点，且BC＝20cm ， ， 一只蚂蚁从点A出发，沿着圆柱体的表面爬行到点P的最短距离为 cm ．
15. 如图，Rt△ABC的斜边AB的中垂线MN与AC交于点M，∠A=15°，BM=2，则△AMB的面积为.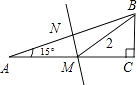
16. 如图，等腰△ABC的底边BC＝20，面积为120，点D在BC边上，且CD＝5，直线EF是腰AC的垂直平分线，若点M在EF上运动，则△CDM周长的最小值为 ．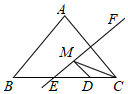
三、解答题
-
17.(1)、；(2)、（x-2）2＝49．18. 已知2a+1的平方根为±3，3a+b-1的算术平方根为4，求a+2b的平方根．19. 如图，已知△ABC中，AD是BC边上的高，CE平分∠ACB，AD与CE相交于点F.∠B=65°，∠AFC=120°，求∠BAD和∠ACB的度数.
20. 学校要征收一块土地，形状如图所示，∠B＝90°，AB＝20m ， BC＝15m ， AD＝24m ， CD＝7m ， 土地价格为1000元/m2 ， 请你计算学校征收这块地需要多少钱？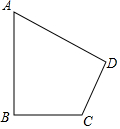
21. 如图，在△ABC中，点D在边BC上，CD=AB，DE∥AB，∠DCE=∠A.求证：DE=BC.
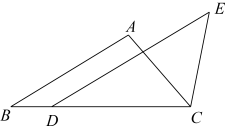22. 如图，折叠长方形一边AD，点D落在BC边的点F处，BC=10cm，AB=8cm，求：
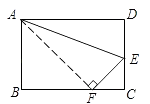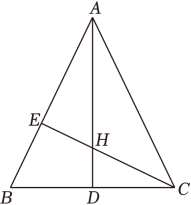
(1)、FC的长；(2)、EF的长．23. 如图，△ABC中，∠ACB＝90°，BC的垂直平分线交AB于点D ， 垂足为E ．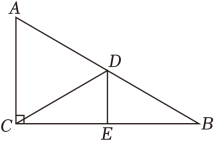
(1)、若∠A＝50°，求∠DCB和∠ADC的度数；(2)、若∠B＝30°，BD＝7，求△ACD的周长．24. 如图，△ABC是等腰三角形，AB＝AC ， ∠BAC＝45°，AD和CE是高，它们相交于H ， 求证：AH＝2BD ．
