人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——12.1全等三角形
试卷更新日期：2023-12-12 类型：复习试卷
一、选择题
-
1. 下列命题属于假命题的是（ ）A、全等三角形的对应边相等． B、全等三角形的对应角相等． C、三个角分别相等的两个三角形全等. D、三条边分别相等的两个三角形全等．2. 如图。△ABC≌△DEC．若∠DCB=85°，∠BCE=40°，则∠ACE的度数为（ ）
A、5° B、10° C、15° D、20°3. 已知图中的两个三角形全等，则∠1等于（ ）
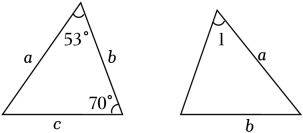A、57° B、53° C、60° D、70°4. 如图， ， ， ， ， 则的度数是（ ）
A、60° B、65° C、70° D、75°5. 嘉嘉、淇淇和笑笑在学习全等三角形时，关于“全等形”提出了三种不同的说法，嘉嘉说；形状、大小相同的图形是全等形，淇淇说：能够完全重合的图形是全等形，笑笑说：各边都相等的图形是全等形.他们的说法中，正确的有（ ）A、0个 B、1个 C、2个 D、3个6. 有下列说法：①能够重合的两个三角形是全等三角形；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长相等，面积相等．其中正确的是（ ）
A、①②③ B、①②④ C、②③④ D、①②③④7. 如图， ， 点和点是对应顶点，点和点是对应顶点，过点作 ， 垂足为点 ， 若 ， 则的度数为（ ）
A、30° B、25° C、35° D、65°8. 下列汽车标志中，不是由多个全等图形组成的是（ ）A、
B、
C、
D、
9. 已知≌ ， ， ， 则的度数为（ ）A、 B、 C、 D、10. 如图，点B在线段AD上，△ABC≌△EBD， AB=2cm， BD＝5cm，则CE的长度为（ ）
A、2cm B、2.5cm C、3cm D、5cm二、填空题
-
11. 两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=4，DO=1，平移距离为2，则阴影部分面积为
12. 如图，点A在DE上，△ABC≌△EDC，若∠BAC=55°，则∠ACE的大小为
13. 如图，四边形ABCD的对角线AC，BD相交于点O， ， 下列结论：①；②；③；④.其中正确结论的序号是.
14. 如图，、、在同一直线上，≌ ， ， 那么度.
15. 如图，已知≌ ， ， 则 度．
三、解答题
-
16. 如图，点A ， B ， C ， D在同一条直线上，AB=CD，AE＝DF ， CE＝BF ． 求证：∠E＝∠F ．
17. 如图，已知 ， 点在线段上，与交于点 ， 且 ． 求证： ．
18. 已知：如图， ， ， ， 求证： ．
19. 如图，AB＝CD，AF＝CE，BE⊥AC于E，DF⊥AC于F．求证：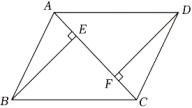
(1)、△ABE≌△CDF．(2)、AD∥BC．20. 如图，BD⊥AC于D，CE⊥AB于E，BD，CE交于O，OB＝OC．求证：∠1＝∠2．
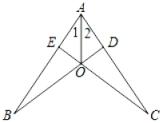21. 如图，点E是等边三角形ABC的高AD上一点，∠EBF＝60°，∠BCF＝30°，求证：△BEF是等边三角形．
22. 如图，AB∥CD ， M是AD的中点，BM⊥CM ， 连接BC ．
(1)、求证：CM平分∠BCD；(2)、探究BC、CD、AB之间的数量关系．23. 如图（1），AB=4cm，AC⊥AB，BD⊥AB，AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．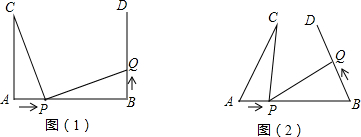
(1)、若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；(2)、如图（2），将图（1）中的“AC⊥AB ， BD⊥AB”改为“∠CAB=∠DBA=60°”其他条件不变．设点Q的运动速度为xcm/s ， 是否存在实数x ， 使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由。