山东省济南市长清区2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2023-12-12 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，共40分.）

1. 25的算术平方根是（）

A、5 B、±5 C、± $\sqrt{5}$ D、 $\sqrt{5}$

查看试题解析
2. 下列是无理数的是（　　）

A、 $\sqrt[3]{27}$ B、π C、 $\sqrt{4}$ D、0.16

查看试题解析
3. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列式子正确的是（　　）

A、 $\sqrt{49} = \pm 7$ B、（-3）²＝-3² C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$

查看试题解析
5.
象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为（4，3），（﹣2，1），则表示棋子“炮”的点的坐标为（　　）

A、（﹣3，3） B、（3，2） C、（0，3） D、（1，3）

查看试题解析
6. 点A（1，y₁）、B（2，y₂）都在一次函数y＝-2x+3的图象上，则y₁、y₂的大小关系是（　　）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不确定

查看试题解析
7. 已知AB∥x轴，AB＝3，点A的坐标为（-1，3），则点B的坐标为（　　）

A、（2，3） B、（-4，3） C、（-1，6）或（-1，0） D、（-4，3）或（2，3）

查看试题解析
8. 一次函数y＝kx+b中，y随x的增大而减小，且kb＜0，则该函数图象大致是（　　）

A、 B、 C、 D、

查看试题解析
9. 如图所示，A（2 $\sqrt{2}$ ， 0），AB＝3 $\sqrt{2}$ ，以点A为圆心，AB长为半径画弧交x轴负半轴于点C ，则点C的坐标为（　　）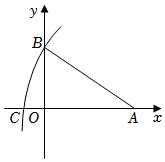

A、（3 $\sqrt{2}$ ， 0） B、（ $\sqrt{2}$ ， 0） C、（- $\sqrt{2}$ ， 0） D、（-3 $\sqrt{2}$ ， 0）

查看试题解析
10. 在平面直角坐标系xOy中，对于P ， Q两点给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P ， Q两点为“等距点”．如图中的P ， Q两点即为“等距点”．若点A的坐标为（-3，1），点B的坐标为B（m ， m+6），且A ， B两点为“等距点”，则点B的坐标为（　　）

A、（3，9） B、（-3，3） C、（-9，-3） D、（-9，3）

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分.）

11. $- \frac{1}{8}$ 的立方根是．

查看试题解析
12. 若点P（m+1，m-1）在y轴上，则m的值为．

查看试题解析
13. 秦兵马俑的发现被誉为“世界第八大奇迹”，兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 $\frac{\sqrt{5} - 1}{2}$ ，则 $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ ．（选填“＞”，“＜”，“＝”）．

查看试题解析
14. 学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示， $l_{1}$ 和 $l_{2}$ 分别表示两人到小亮家的距离 $s (k m)$ 和时间 $t (h)$ 的关系，则出发h后两人相遇．

查看试题解析
15. 如图，直线 $y = - \frac{3}{4} x - 3$ 与x轴、y轴分别交于点A和点B ，点C是x轴上的一个动点，将△ABC沿BC所在直线折叠后，点A恰好落在y轴上点D处，则点C的坐标为．

查看试题解析
16. 如图，在平面直角坐标系xOy中，A（2，0），B（10，0），点P为y轴正半轴上的一个动点，以线段PA为边在PA的右上方作等边△APQ ，连接QB ，在点P运动的过程中，线段QB长度的最小值为．

查看试题解析

三、解答题（本大题共10小题，共86分）

17. 计算：

(1)、 $\frac{\sqrt{27} - \sqrt{48}}{\sqrt{3}}$ ；

(2)、 $\frac{\sqrt{15} \times \sqrt{3}}{\sqrt{5}}$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{12} - 6 \sqrt{\frac{1}{3}} + \sqrt{8}$ ；

(2)、 ${(\sqrt{5} - 1)}^{2} + (\sqrt{5} + 2) (\sqrt{5} - 2)$ ．

查看试题解析
19. 计算： $\sqrt{8} + | \sqrt{3} - 2 | - {(- \frac{1}{2})}^{- 1} + {(π - 2023)}^{0}$ ．

查看试题解析
20. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，-2）、B（2，-4）、C（4，-1）．
⑴作出△ABC关于y轴对称的△A₁B₁C₁；
⑵写出点的坐标：A₁（　 ▲ 　），B₁（　 ▲ 　），C₁（　 ▲ 　）；
⑶在x轴上找一点P ，使PA+PC最小，标出点P的位置（不写画法，保留作图痕迹）．

查看试题解析
21. 如图，已知直线y＝kx+b的图象经过点A（0，-4），B（3，2），且与x轴交于点C ．

(1)、求一次函数的解析式；

(2)、观察图象，直接写出方程kx+b＝0的解为；

(3)、求△AOB的面积．

查看试题解析
22. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a ， 0），点C的坐标为（0，b），且a、b满足 $\sqrt{(a - 4)}$ +|b-6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动．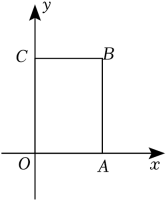

(1)、点B的坐标为；当点P移动4秒时，写出点P的坐标．

(2)、若点Q从点C以每秒1个单位长度的速度沿着C→B→A→O→C的线路移动，点Q与点P同时出发，几秒后点Q与点P第一次相遇？

查看试题解析
23. 河南信阳毛尖是中国十大名茶之一，因其成品紧密如尖故名毛尖．某公司采购员到信阳茶叶市场购买某品牌毛尖茶，商家推出了两种购买方式：

会员卡费用（元/张）
茶叶价格（元/kg）
方式一：金卡会员
500
1600
方式二：银卡会员
200
1800
设该公司此次购买茶叶xkg ，按方式一购买茶叶的总费用为y₁元，按方式二购买茶叶的总费用为y₂元．

(1)、请直接写出y₁ ， y₂关于x的函数解析式；

(2)、若按方式一购买茶叶的总费用和按方式二购买茶叶的总费用相同，求该公司此次购买茶叶的质量；

(3)、若该公司此次购买茶叶的总预算为6500元，则按哪种方式购买可以获得更多的茶叶？

查看试题解析
24. 小明在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求2a²-8a+1的值．他是这样分析与解的：
∵ $a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，
∴ $a - 2 = - \sqrt{3}$ ，
∴（a-2）²＝3，a²-4a+4＝3，
∴a²-4a＝-1，
∴2a²-8a+1＝2（a²-4a）+1＝2×（-1）+1＝-1．
请你根据小明的分析过程，解决如下问题：

(1)、①化简 $a = \frac{1}{\sqrt{2} - 1}$ ＝　 ▲ 　；
②当 $a = \frac{1}{\sqrt{2} - 1}$ 时，求3a²-6a-1的值．

(2)、化简 $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + ⋯ + \frac{1}{\sqrt{121} + \sqrt{119}}$ ．

查看试题解析
25. 【复习旧知】结合数轴与绝对值的知识回答下列问题：
数轴上表示4和1的两点之间的距离是3；而|4-1|＝3；表示-3和2两点之间的距离是5；而|-3-2|＝5；表示-4和-7两点之间的距离是3；而|-4-（-7）|＝3．
一般地，数轴上表示数m和数n的两点之间的距离公式为|m-n|．

(1)、数轴上表示数-4的点与表示-1的点之间的距离为．

(2)、【探索新知】
如图①，我们在“格点”直角坐标系上可以清楚看到：要找AB或DE的长度，显然是化为求Rt△ABC或Rt△DEF的斜边长．
下面：以求DE为例来说明如何解决．
从坐标系中发现：D（-7，5），E（4，-3）．所以DF＝|5-（-3）|＝8，EF＝|4-（-7）|＝11，所以由勾股定理可得： $D E = \sqrt{8^{2} + 1 1^{2}} = \sqrt{185}$ ．
在图②中：设A（x₁ ， y₁），B（x₂ ， y₂），试用x₁ ， y₁ ， x₂ ， y₂表示：AC＝， BC＝， AB＝．
得出的结论被称为“平面直角坐标系中两点间距离公式”．

(3)、【学以致用】请用此公式解决如下题目：
已知A（-2，3）、B（4，-5），试求A、B两点间的距离．

(4)、已知一个三角形各顶点坐标为A（-1，1）、B（-3，3）、C（2，4），请判定此三角形的形状，并说明理由．

查看试题解析
26. 如图，在平面直角坐标系中，直线l₁：y＝ $\frac{3}{4}$ x与直线l₂：y＝kx+b（k≠0）相交于点A（a ， 3），直线l₂与y轴交于点B（0，-5）．

(1)、求直线l₂的函数解析式；

(2)、将△OAB沿直线l₂翻折得到△CAB ，使点O与点C重合，AC与x轴交于点D ．求证：AC∥OB；

(3)、在直线BC下方是否存在点P ，使△BCP为等腰直角三角形？若存在，直接写出点P坐标；若不存在，请说明理由．

查看试题解析

	会员卡费用（元/张）	茶叶价格（元/kg）
方式一：金卡会员	500	1600
方式二：银卡会员	200	1800