人教版2023-2024年数学七年级第一学期期末扫盲清障复习卷——期末综合测试卷

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列说法正确的是（）

A、代数式 $- \frac{x y^{2}}{5}$ 不是整式 B、单项式x的系数为0 C、单项式-2πxyz²的次数为5 D、多项式a²-2b的次数为2

查看试题解析
2. 开学第一节课赵老师给每人发了一个正方体，它的六个面分别标注有“一切皆有可能”，表面展开后如图 $.$ 那么在原正方体中，“一”的对面是（）

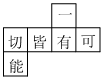A、能 B、可 C、皆 D、切

查看试题解析
3. 若两个非零有理数 $a ， b$ ，满足 $| a | = a ， | b | = - b ， a + b < 0$ ，则 $a ， b$ 的取值符合题意的是（）

A、 $a = 2 ， b = - 1$ B、 $a = - 2 ， b = 1$ C、 $a = 1 ， b = - 2$ D、 $a = - 1 ， b = - 2$

查看试题解析
4. 某种速冻水饺的储藏温度是 $- 18 \pm 2 ℃$ ，四个冷藏室的温度如下，则不适合储藏此种水饺是（）

A、 $- 17 ℃$ B、 $- 22 ℃$ C、 $- 18 ℃$ D、 $- 19 ℃$

查看试题解析
5. 下列说法不正确的是（）

A、0既不是正数，也不是负数 B、1是绝对值最小的有理数 C、一个有理数不是整数就是分数 D、0的绝对值是0

查看试题解析
6. 下列说法错误的是（）

A、 $2 x^{2} - 3 x y - 1$ 是二次三项式 B、 $- x + 1$ 的项是 $- x$ 、1 C、 $- x^{2} y$ 的系数是 $- 1$ D、 $- 2 a b^{2}$ 是二次单项式

查看试题解析
7. 若关于 $x$ ， $y$ 的单项式 $3 x^{5} y^{m}$ 与 $- 2 x^{n} y^{7}$ 的和仍为単项式，则 $m - n$ 的值为（　　）

A、2 B、5 C、7 D、9

查看试题解析
8. 下列是根据等式的性质进行变形，正确的是（）

A、若 $x = y$ ，则 $x + 5 = y - 5$ B、若 $a - x = b + x$ ，则 $a = b$ C、若 $a x = a y$ ，则 $x = y$ D、若 $\frac{x}{2} = \frac{y}{2}$ ，则 $x = y$

查看试题解析
9. 一项工程，甲独做3天完成，乙独做7天完成，两人共同合作，需x天完成，可列方程（）

A、3x+7x=1 B、 $\frac{x}{3} + \frac{x}{7}$ =1 C、( $\frac{1}{3} - \frac{1}{7}$ )x=1 D、x=( $\frac{1}{3} - \frac{1}{7}$ )-1

查看试题解析
10. 有两根木条AB和CD，AB的长为80 cm，CD的长为130 cm，在它们的中点处各有一个小圆孔M，N(圆孔直径忽略不计，M，N抽象成两个点)，将它们的一端重合，放置在同一条直线上，此时两根木条的小圆孔之间的距离MN=（）

A、25 cm B、105 cm C、25cm或105cm D、50cm或210cm

查看试题解析

二、填空题

11. 节约是一种美德，节约是一种智慧，据不完全统计，全国每年浪费食物总量折合粮食可养活约350000000人，数据350000000用科学记数法表示为

查看试题解析
12. 在数轴上点A、B表示的数分别是-3和5，则线段AB长是。

查看试题解析
13. 一跳蚤在一直线上从O点开始，第1次向右跳1个单位长度，紧接着第2次向左跳2个单位长度，第3次向右跳3个单位长度，第4次向左跳4个单位长度……依此规律跳下去，当它跳第99次落下时，落点处离O点的距离是个单位长度．

查看试题解析
14. 如果三角形的第一条边长为（3a+2b）cm，第二条边长比第一条边长短（a-b）cm，第三条边长比第一条边长的2倍少2b（cm），则这个三角形的周长是cm．

查看试题解析
15. 小明和小红制作小红旗，100个小红旗两人合作20分钟完成，已知小明每分钟做2个，则小红每分钟做个．

查看试题解析

三、计算题

16. 计算：

(1)、（-6）+5+（-2）

(2)、-1²+2×（-3）²-4÷（ $- \frac{2}{3}$ ）

(3)、2x-3y+ （5x+4y）

(4)、3（2x²-x+2）-2（1-3x²+x）

查看试题解析
17. 解方程：

(1)、 $3 (20 - y) = 6 y - 4 (y - 11)$

(2)、 $\frac{0.4 x + 3}{0.2} - 2 = \frac{0.45 - x}{0.3}$

查看试题解析

四、解答题

18. 已知代数式A=2x²+3xy+2y，B=x²-xy+y ．

(1)、求A-2B；

(2)、当x=-1，y=3时，求A-2B的值．

查看试题解析

19. 某市自2023年1月起，对餐饮用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：

	月用水量（立方米）	水价（元/立方米）
第一级	50立方米以下（含50立方米）的部分	4.6
第二级	50立方米-150立方米（含150立方米）的部分	6.5
第三级	150立方米以上的部分	8

(1)、受特殊情况影响，某饭店4月份用水量为20立方米，则该饭店4月份需交的水费为元．

(2)、某饭店9月份用水量为a（50<a≤150）立方米，则该饭店9月份应交的水费为元，（用含a的代数式表示）

(3)、某饭店11月份交水费1120元，求该饭店11月份的用水量．

查看试题解析

20. 某司机某天下午在一条南北向的马路上开出和车．如果规定向南为正，向北为负，该司机连续接送5位乘客的行程（单位：千米）如下： $+ 4 ， - 3 ， - 5 ， + 2 ， + 6$ ，

(1)、该司机下午接送这5位乘客到达目的地，行程一共是多少千米？

(2)、若规定出租车的起步价为8元，起步行程为3千米以内（包括3千米），超过的部分每千米2元，请问该司机上午一共收入多少车费？

查看试题解析
21. 已知有理数a ， b ， c在数轴上的位置如图．

(1)、判断正负，用“＞”或“＜”填空．
c－b0，a－b0，c－a0．

(2)、化简|c－b|+|a－b|－|c－a|．

查看试题解析
22. 如图，直线AB，CD相交于点O，OE，OF是两条射线，∠BOE=50°，OD平分∠AOE．

(1)、求∠AOD的度数．

(2)、若∠BOF与∠BOE互余，求∠COF的度数．

查看试题解析
23. 如图，已知A、B、C是数轴上三点，点O为原点，点C表示的数为6， $B C = 4$ ， $A B = 12$ ．

(1)、数轴上点A表示的数为， B表示的数；

(2)、动点P、Q分别从A、C同时出发，沿数轴向右匀速运动．点P的速度是每秒6个单位长度，点Q的速度是每秒3个单位长度，点M为AP的中点，点N在线段CQ上，且 $C N = \frac{1}{3} C Q$ ．设运动时间为 $t (t > 0)$ 秒．
①数轴上点M表示的数为 ▲ ， N表示的数为 ▲ （用含t的式子表示）；
②当M、B、N三个点中的其中一个点是另两点构成的线段的中点的时候，求t的值．

查看试题解析