人教版2023-2024年数学七年级第一学期期末扫盲清障复习卷——4.2直线、射线、线段
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 下列四个生活中产生的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵的位置,就能确定同一行树所在的直线;③从A地到B架设电线,总是尽可能沿着线段AB方向架设;④把弯曲的公路改直,就能缩短路程。
其中可用公理“两点之间,线段最短”来解释的现象有( )
A、①② B、①③ C、②③ D、③④2. 如果线段 , M是平面内一点,且 , 那么下列说法中正确的是( )A、点M一定在线段AB上 B、点M一定不在线段AB上 C、点M有可能在线段AB上 D、点M一定在直线AB上3. 如图, , C为AB的中点,点D在线段AC上,且 , 则DC的长度为( )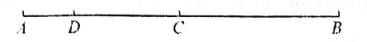 A、1 B、2 C、3 D、44. 已知线段 , 点是直线上一点, , 若是的中点,是的中点,则线段的长度是( )A、 B、 C、 D、或5. 下列各图中,两线能相交的是( )A、
A、1 B、2 C、3 D、44. 已知线段 , 点是直线上一点, , 若是的中点,是的中点,则线段的长度是( )A、 B、 C、 D、或5. 下列各图中,两线能相交的是( )A、 B、
B、 C、
C、 D、
D、 6. 开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为( )A、两点之间,线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度,叫做这两点之间的距离7. 下列几何图形与相应语言描述相符的有( )
6. 开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为( )A、两点之间,线段最短 B、经过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度,叫做这两点之间的距离7. 下列几何图形与相应语言描述相符的有( )如图 , 直线、相交于点 如图 , 直线与线段没有公共点如图 , 延长线段 如图 , 直线经过点
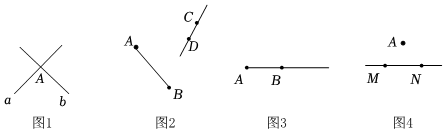 A、个 B、个 C、个 D、个8. 如图所示,由济南始发终点至青岛的某一次列车,运行途中停靠的车站依次是:济南淄博潍坊青岛,那么要为这次列车制作的单程火车票种.( )
A、个 B、个 C、个 D、个8. 如图所示,由济南始发终点至青岛的某一次列车,运行途中停靠的车站依次是:济南淄博潍坊青岛,那么要为这次列车制作的单程火车票种.( ) A、 B、 C、 D、9. 经过同一平面内的A、B、C三点中的任意两点,可以作出____直线( )A、1条 B、3条 C、1条或3条 D、无数条10. 如图,C是AB的中点,D是BC的中点,则下列等式中成立的有( )
A、 B、 C、 D、9. 经过同一平面内的A、B、C三点中的任意两点,可以作出____直线( )A、1条 B、3条 C、1条或3条 D、无数条10. 如图,C是AB的中点,D是BC的中点,则下列等式中成立的有( )
①CD=AD-BD;②CD=AD-BC;③2CD=2AD-AB;④CD=AB.
A、①② B、②③ C、①③ D、②④二、填空题
-
11. 如图,建筑工人在砌墙时,经常在两个墙角的位置分别插一根木桩,然后拉一条直的参照线,其运用的数学原理是
 12. 如图,BC=4cm , BD=7cm , 点D是AC的中点,则AC=cm .
12. 如图,BC=4cm , BD=7cm , 点D是AC的中点,则AC=cm . 13. 延长线段AB到点C,使BC=AB,反向延长AC到点D,使AD=AC,则CD=AB.14. 如图所示,已知线段AD=AB,AE=AC,BC=4,则DE=.
13. 延长线段AB到点C,使BC=AB,反向延长AC到点D,使AD=AC,则CD=AB.14. 如图所示,已知线段AD=AB,AE=AC,BC=4,则DE=. 15. 已知数轴上点A , B所对应的数分别是1,3,从点A出发向负方向移动2个单位长度得到点C , 从点B出发向正方向移动2个单位长度得到点D , 则点C , D之间的距离为个单位长度.
15. 已知数轴上点A , B所对应的数分别是1,3,从点A出发向负方向移动2个单位长度得到点C , 从点B出发向正方向移动2个单位长度得到点D , 则点C , D之间的距离为个单位长度.三、作图题
-
16. 如图,已知有不在同一条直线上的四点A,B,C,D,请按下面的要求画图.

(1)画射线AB.
(2)画线段BC.
(3)画直线AC,BD,相交于点O.四、解答题
-
17. 如图,数轴上有A、B、C三个点,A、B、C对应的数分别是a、b、10,且 , 动点P从点A出发,以每秒1个单位长度的速度向终点C运动,设运动时间为t秒.
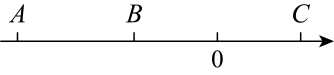 (1)、求a、b的值;(2)、若点P到点A的距离是点P到点B的距离的2倍,求点P对应的数;(3)、当点P运动到点B时,点Q从点A出发,以每秒3个单位长度的速度向点C运动,点Q到达点C后,再立即以同样的速度返回,向终点A运动.若点P在点Q的左侧,请直接写出当点Q开始运动后第几秒时,P、Q两点之间的距离为4.18. 如图,已知点A、B在数轴上分别对应-12和15,点O为原点,点P从点A出发,以每秒2个单位长度的速度向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度向终点A运动,设运动的时间为t秒(t>0) .
(1)、求a、b的值;(2)、若点P到点A的距离是点P到点B的距离的2倍,求点P对应的数;(3)、当点P运动到点B时,点Q从点A出发,以每秒3个单位长度的速度向点C运动,点Q到达点C后,再立即以同样的速度返回,向终点A运动.若点P在点Q的左侧,请直接写出当点Q开始运动后第几秒时,P、Q两点之间的距离为4.18. 如图,已知点A、B在数轴上分别对应-12和15,点O为原点,点P从点A出发,以每秒2个单位长度的速度向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度向终点A运动,设运动的时间为t秒(t>0) . (1)、线段AB的长度为 ;(2)、动点Q在数轴上表示的数为;(用含t的代数式表示)(3)、当点P、Q两点之间的距离为3时,求t的值:(4)、当点P,O,Q中一个点到另外两个点(其中两个点重合时除外)的距离相等时,直接写出t的值.19. 结合数轴与绝对值的知识回答下列问题:
(1)、线段AB的长度为 ;(2)、动点Q在数轴上表示的数为;(用含t的代数式表示)(3)、当点P、Q两点之间的距离为3时,求t的值:(4)、当点P,O,Q中一个点到另外两个点(其中两个点重合时除外)的距离相等时,直接写出t的值.19. 结合数轴与绝对值的知识回答下列问题: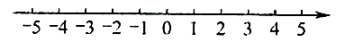 (1)、数轴上表示1和4的两点之间的距离是;表示和2的两点之间的距离是;表示和的两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于。(2)、如果表示数a和的两点之间的距离是3,那么。(3)、若数轴上表示数a的点位于与2之间,则的值是。(4)、当时,的值最小,最小值是。20. A、B、C、D四个车站的位置如图所示,求:
(1)、数轴上表示1和4的两点之间的距离是;表示和2的两点之间的距离是;表示和的两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于。(2)、如果表示数a和的两点之间的距离是3,那么。(3)、若数轴上表示数a的点位于与2之间,则的值是。(4)、当时,的值最小,最小值是。20. A、B、C、D四个车站的位置如图所示,求: (1)、A、D两站的距离;(2)、A、C两站的距离.21. 如图,点B,C在线段AD上,且AB:BC:CD=2:3:4,M是线段AC的中点,N是线段CD的中点,且MN=9.求BD的长.
(1)、A、D两站的距离;(2)、A、C两站的距离.21. 如图,点B,C在线段AD上,且AB:BC:CD=2:3:4,M是线段AC的中点,N是线段CD的中点,且MN=9.求BD的长. 22. 如图,线段AB被点C,D分成2:4:7三部分,M,N分别是AC,DB的中点,若MN=17 cm,求BD的长.
22. 如图,线段AB被点C,D分成2:4:7三部分,M,N分别是AC,DB的中点,若MN=17 cm,求BD的长. 23. 阅读下面材料:
23. 阅读下面材料:在数轴上2与-1所对应的两点之间的距离为|2-(-1)|=3;
在数轴上-2与3所对应的两点之间的距离为|-2-3|=5;
在数轴上-3与-1所对应的两点之间的距离为|(-1)-(-3)|=2.
归纳:在数轴上点A,B分别表示数a,b,则A,B两点之间的距离AB=|a-b|或|b-a|.
回答下列问题:
(1)、数轴上表示数x和1的两点之间的距离表示为;数轴上表示数x和的两点之间的距离表示为|x+2|;(2)、试说明当表示数x的点在-2与3的对应点之间移动时,|x-3| +|x+2|的值总是一个固定的值,并求出这个固定值.
-