人教版（吉林地区）初中数学2023-2024学年八年级上学期期末模拟卷（一）

试卷更新日期：2023-12-12 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 等腰三角形一边长9cm，另一边长4cm，它的第三边是（） cm．

A、4 B、9 C、4或9 D、不能确定

查看试题解析
3. 如果 x，y 同时扩大为原来的2倍，那么分式 $\frac{x^{2} + y^{2}}{x + y}$ 的值变成原来的（）

A、2倍 B、4倍 C、 $\frac{1}{2}$ D、不变

查看试题解析
4. 如图，美美不小心在课后作业的第1题滴了一点墨水，留下一道残缺不全的题目，则被墨水覆盖的部分为（）

A、 $x^{3} - x^{2} + x$ B、 $- x^{3} - x^{2} + x$ C、 $- x^{3} + x^{2} - x$ D、 $x^{3} + x^{2} - x$

查看试题解析
5. 如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样设计蕴含的数学依据是（　　）

A、两直线平行，内错角相等 B、垂线段最短 C、两点之间，线段最短 D、三角形具有稳定性

查看试题解析
6. 如图，CE是△ABC的外角∠ACD的平分线，若∠B＝35°，∠ACE＝60°，则∠A＝（　　）

A、35° B、95° C、85° D、75°

查看试题解析
7. 如图，在由4个相同的小正方形拼成的网格中，∠2-∠1=（）

A、60° B、75° C、90° D、105°

查看试题解析
8. 如图， $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ 、 $B M$ 是 $A C$ 边的中线，有 $A D ⊥ B M$ ；垂足为点 $E$ 交 $B C$ 于点 $D$ ．且 $A H$ 平分 $∠ B A C$ 交 $B M$ 于 $N$ ．交 $B C$ 于 $H$ ．连接 $D M$ ．则下列结论：
① $∠ A M B = ∠ C M D$ ；② $H N = H D$ ；③ $B N = A D$ ；④ $∠ B N H = ∠ M D C$ ；

错误的有（）个．

A、0 B、1 C、3 D、4

查看试题解析

二、填空题

9. 计算 $1 \div (- a) \cdot \frac{1}{a}$ 的结果是.

查看试题解析
10. 一项工程，若甲、乙两人合作需要 $m$ 小时完成，甲单独做需要 $n$ 小时完成，那么乙单独做需要小时完成．

查看试题解析
11. 已知2^a=3，2^b=5， 2^c=15，那么a、b、c之间满足的等量关系是

查看试题解析
12. 如图，在△ABC中，AB= AC，分别以点B和点C为圆心。以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧交于点D，作直线AD交BC于点E．若∠BAE=44°，则∠BAC=度．

查看试题解析
13. 如图，已知AD、DE、EF分别是△ABC、△ABD、△AED的中线，若S_△_ABC＝24cm² ，则阴影部分△DEF的面积为．

查看试题解析
14. 如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（ -2，0），点A的坐标为（-6，3），则B点的坐标是

查看试题解析

三、计算题

15. 因式分解：

(1)、ax²-a；

(2)、6xy²-9x²y-y³ ．

查看试题解析
16. 已知(a+b)²=17，(a- b)²=13，
求：

(1)、a²+b²的值；

(2)、ab的值．

查看试题解析

四、作图题

17. 如图，已知△ABC的顶点分别为A （-2，2），B （-4，5），C（-5，1）．
⑴作出△ABC关于x轴对称的图形△A₁B₁C₁ ，并写出点B₁的坐标；
⑵若点P（a，b）是△ABC内部一点，则点P关于y轴对称的点的坐标是
⑶在x轴上找一点P，使得AP+CP最小（画出图形，找到点P的位置）．

查看试题解析

五、解答题

18. 已知关于x的分式方程 $\frac{2 x - m}{x - 1} - \frac{3}{1 - x} = 1$ 的解是正数，求m的取值范围.

查看试题解析
19. 尺规作图：经过已知直线外一点作已知直线的垂线．
已知：直线AB和AB外一点C．
求作： AB的垂线，使它经过点C．
作法：（1）任意取一点K，使点K和点C在AB的两旁；（2）以点C为圆心，CK长为半径作弧，交AB于点D和E；（3）分别以点D和点E为圆心，大于 $\frac{1}{2}$ DE的长为半径作弧，两弧相交于点F；（4）作直线CF，连接CD、CE、EF、DF．
根据以上作法证明直线CF就是所求作的垂线．

查看试题解析
20. 如图，在等边△ABC中，D，E分别是BC，AC上的点，且AE=CD．AD与BE交于点N，BM⊥AD于点M．
求证：

(1)、△ABE≌△CAD；

(2)、MN= $\frac{1}{2}$ BN．

查看试题解析
21. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式。
例如图1可以得到(a+b)²=a²+2ab+b² ，请解答下列问题：

(1)、图2所表示的数学等式为

(2)、利用(1)得到的结论，解决问题：若a+b+c=12，a²+b²+c²=60，求ab+ac+bc的值；

(3)、如图3，将两个边长分别为a和b的正方形拼在一起，B，C，D三点在同一直线上，连接AE、EG，若两正方形的边长满足a+b=15，ab=35，求阴影部分面积．

查看试题解析
22. 如图，在△ABC中，点D是BC的中点，DE⊥AB ， DF⊥AC ． E、F为垂足，BE＝CF ．求证：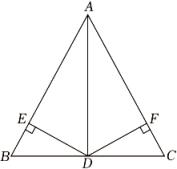

(1)、DE＝DF；

(2)、连接AD ，这时AD平分∠BAC吗？请说明理由．

查看试题解析

六、实践探究题

23. 醴陵市委市政府顺应百万醴陵人民夙愿，全方位推进“瓷城古韵 $\cdot$ 一江两岸”老城改造，并将其列入十大民生工程项目 $.$ 目前，该项目已完成渌江古桥、状元芳洲、渌江广场、南岸风光带、南街酒吧等建设并投入使用 $.$ 即将启动泗州寺、清代文庙、千年县衙、百年学府门楼、渌水人家等子项目建设 $.$ 醴陵市招投标中心接到甲、乙两个工程队关于清代文庙的投标书，甲、乙工程队施工一天的工程费用分别为 $21$ 万元和 $16$ 万元，市招投标中心根据甲、乙两工程队的投标书测算，应有三种施工方案：
方案一：甲队单独做这项工程刚好如期完成；

方案二：乙队单独做这项工程，要比规定日期多 $5$ 天；

方案三：若甲、乙两队合做 $4$ 天后，余下的工程由乙队单独做，也正好如期完成．

根据以上方案提供的信息，在确保工期不耽误的情况下，你认为哪种方案最节省工程费用，通过计算说明理由．

查看试题解析
24. 小明发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等三角形，小明把具有这个规律的图形称为“手拉手”图形．

(1)、问题发现：在图1的“手拉手”图形中，若△ABC和△ADE均是顶角为40°的等腰三角形，BC ， DE分别是底边，求证：BD＝CE；

(2)、拓展探究：如图2，若△ABC和△CDE均是等边三角形，点A ， D ， E在同一条直线上，连接BE ，则∠AEB＝°，线段BE与AD之间的数量关系是；

(3)、解决问题：如图3，若△ABC和△DCE均是等腰直角三角形，∠ACB＝∠DCE＝90°，点A ， D ， E在同一条直线上，CM为△DCE中DE边上的高，连接BE ，请求出∠AEB的度数，写出线段CM ， AE ， BE之间的数量关系，并说明理由．

查看试题解析