人教版2023-2024年数学七年级第一学期期末扫盲清障复习卷——3.2移项、合并同类项解一元一次方程

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列解方程中，移项正确的是（）

A、由5+x=18，得x=18+5 B、由5x+ $\frac{1}{3}$ =3x，得5x-3x= $\frac{1}{3}$ C、由 $\frac{1}{2}$ x+3= $- \frac{3}{2}$ x-4，得 $\frac{1}{2}$ x+ $\frac{3}{2}$ x=-4-3 D、由3x-4=6x，得3x+6x=4．

查看试题解析
2. 若式子-2a+1与a-2的值相等，则a等于（）

A、1 B、2 C、-1 D、-2

查看试题解析
3. 嘉琪在进行解方程的思维训练，其中有一个方程“2y- $\frac{1}{2}$ = $\frac{1}{2}$ y+■”中的■没印清晰，嘉琪问老师，老师只是说：“■是一个有理数，该方程的解与当×= 2时代数式5(x-1)-2(x- 2)-4的值相同．”嘉琪很快补上了这个有理数．你认为嘉琪补的这个有理数是（）

A、1 B、-1 C、2 D、-2

查看试题解析
4. 根据如图所示的程序计算函数y的值，若输入x的值是7，则输出y的值是 $- 2$ ，若输入x的值是 $- 8$ ，则输出y的值是（）

A、5 B、19 C、0 D、21

查看试题解析
5. 已知 $(k - 1) x^{∣ k ∣} + 3 = 0$ 是关于 $x$ 的一元一次方程．则此方程的解是（）

A、-1 B、 $- \frac{3}{2}$ C、 $\frac{3}{2}$ D、±1

查看试题解析
6. 若关于 $x$ 的方程 $k x - 2 x = 14$ 的解是正整数，则 $k$ 的整数值有个．（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 规定新运算“⊕”：对于任意实数a、b都有 $a \oplus b = a b - a + b - 1$ ，例如： $2 \oplus 5 = 2 \times 5 - 2 + 5 - 1$ ，则方程 $2 \oplus x = 1$ 的解是（）

A、 $\frac{2}{3}$ B、1 C、 $\frac{4}{3}$ D、 $\frac{5}{3}$

查看试题解析
8. 已知 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ 是方程 $m x + 2 y = 5$ 的解，则 $m$ 的值是（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、-2 D、2

查看试题解析
9. 如果四个不同的正整数 $m$ ， $n$ ， $p$ ， $q$ 满足 $(4 - m) (4 - n) (4 - p) (4 - q) = 9$ ，则 $m + n + p + q$ 等于（）

A、 $12$ B、 $14$ C、 $16$ D、 $18$

查看试题解析
10. 已知方程7x+2=3x-6与x-1=k 的解相同，则3k²-1的值为（）

A、18 B、20 C、26 D、-26

查看试题解析

二、填空题

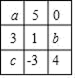
11. 已知方程3x-1=2x+1和方程2x+a=3a+2的解互为倒数，那么a的值是

查看试题解析
12. 如图是正方体的展开图，相对两个面上的数互为倒数，则x＝， y＝．

查看试题解析
13. 若方程2x+a＝1与方程3x-1＝2x+2的解相同，则a的值为．

查看试题解析
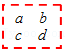14. 如图是一个数表，现用一个矩形在数表中任意框出4个数，当a+b+c+d＝32时，a＝．

查看试题解析
15. 一般情况下 $\frac{m}{2} - \frac{n}{3} = \frac{m - n}{2 - 3}$ 不成立，但有些数可以使得它成立，例如：m＝n＝0.我们称使得 $\frac{m}{2} - \frac{n}{3} = \frac{m - n}{2 - 3}$ 成立的一对数m，n为“神奇数对”，记为（m，n）.若（8，n）是“神奇数对”，且关于x的方程3x-6＝n与2x-1＝3k的解相等，则k的值为.

查看试题解析

三、计算题

16. 解下列方程：

(1)、2x-1=3．

(2)、3-4x=2-x．

(3)、0.2x+1=-1.8x．

(4)、 $\frac{1}{3}$ x=9- $\frac{2}{3}$ x

查看试题解析
17. 解下列方程

(1)、4x = 20

(2)、6x + 6=18

(3)、5x ̶ 6 = 24

(4)、3x - 9 = 3

查看试题解析

四、解答题

18. 若方程 $2 x - 3 = 11$ 与关于 $x$ 的方程 $4 x + 5 = 3 k$ 有相同的解，求 $k$ 的值.

查看试题解析
19. 已知关于x的方程 $a x + 14 = 2 x + a$ 的解是3，求式子 $a^{2} + 2 (a - 3)$ 的值.

查看试题解析
20. 小莹在解关于 $x$ 的方程 $5 a + x = 13$ 时，误将 $+ x$ 看作 $- x$ ，得方程的解为 $x = - 2$ ，求原方程的解为多少？

查看试题解析
21. 如图，乐乐将﹣3，﹣2，﹣1，0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a、b、c分别标上其中的一个数，则a﹣b+c的值是多少？

查看试题解析
22. 若 $x = 1$ 是方程 $2 - \frac{1}{3} (m - x) = 2 x$ 的解，求关于 $y$ 的方程 $m (y - 3) - 2 = m (2 y - 5)$ 的解.

查看试题解析
23. m为何值时，关于x的一元一次方程 $x = 2 x - 3$ 的解与 $4 x - 2 m = 3 x - 1$ 的解相等？

查看试题解析

人教版2023-2024年数学七年级第一学期期末扫盲清障复习卷——3.2移项、合并同类项 解一元一次方程

一、选择题

二、填空题

三、计算题

四、解答题

人教版2023-2024年数学七年级第一学期期末扫盲清障复习卷——3.2移项、合并同类项解一元一次方程