人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——第二十一章综合测试卷

试卷更新日期：2023-12-12 类型：复习试卷

进入出卷网下载

一、选择题

1. 方程x²＝﹣2x+8化为一元二次方程的一般形式后，二次项系数、一次项系数、常数项分别是（　　）

A、1，﹣2，8 B、﹣1，2，8 C、1，2，﹣8 D、1，2，8

查看试题解析
2. 如图，某学校有一块长35米、宽20米的长方形试验田，为了便于管理，现要在中间开辟一横两纵三条等宽的小道，要使种植面积为600平方米．设小道的宽为x米，根据题意可列方程为（）

A、（35-x）（20-2x）=600． B、35×20-35x-20x+2x²=600． C、（35-2x）（20-x）=600． D、35x+2×20x-2x²=600．

查看试题解析
3. 用配方法解一元二次方程x²﹣6x+8＝0配方后得到的方程是（　　）

A、（x+6）²＝28 B、（x﹣6）²＝28 C、（x+3）²＝1 D、（x﹣3）²＝1

查看试题解析
4. 已知方程 $x^{2} + p x + q = 0$ 的两个根分别是2和 $- 3$ ，则 $x^{2} - p x + q$ 可分解为（）

A、 $(x + 2) (x + 3)$ B、 $(x - 2) (x - 3)$ C、 $(x - 2) (x + 3)$ D、 $(x + 2) (x - 3)$

查看试题解析
5. 下列方程中，是一元二次方程的有（    ）个．
$（ 1 ）$ $x^{2} - 18 = 0$        $（ 2 ）$ $3 y^{2} - 4 x = 0$        $（ 3 ）$ $x - \frac{1}{x} = 0$
$（ 4 ）$ $\sqrt{3} x^{2} - x + 1 = 0$        $（ 5 ）$ $(x + 1) (x + 4) = x (x - 2)$        $（ 6 ）$ $(x + 3) (x - 3) + 16 = 0$

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 已知关于x的一元二次方程 $x^{2} + b x + c = 0$ 有一个非零实数根c ，则 $b + c$ 的值为（）

A、1 B、-1 C、0 D、2

查看试题解析
7. 已知关于x的一元二次方程x²-mx+n＝0，其中m，n在数轴上的对应点如图所示，则这个方程的根的情况是（）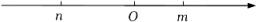

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
8. 已知一元二次方程a（x+m）²+n＝0（a≠0）的两根分别为﹣3，1，则方程a（x+m﹣2）²+n＝0（a≠0）的两根分别为（　　）

A、1，5 B、﹣1，3 C、﹣3，1 D、﹣1，5

查看试题解析
9. 若 $(a + 1) x^{| a - 1 |} - 4 = 0$ 是关于 $x$ 的一元二次方程，则 $a$ 的值为（）

A、 $3$ B、 $- 1$ C、 $0$ D、 $3$ 或 $- 1$

查看试题解析
10. 我国古代著作 $《$ 四元玉鉴 $》$ 记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意为：现请人代买一批椽，这批椽的价钱为 $6210$ 文．如果每株椽的运费是 $3$ 文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问 $6210$ 文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x + 1) x = 6210$ B、 $3$ $(x - 1) = 6210$ C、 $(3 x - 1) x = 6210$ D、 $3 (x - 1) x = 6210$

查看试题解析

二、填空题

11. 已知关于x的一元二次方程（m-1）x²+2mx+m-5=0有实数根，则m的取值范围是

查看试题解析
12. 关于x的一元二次方程 $（ m + 3) x^{2} - 5 x - m^{2} - 5 m - 6 = 0$ 有一个根为0，则m=

查看试题解析
13. 关于x的一元二次方程x²+2x-2=0的两个根分别是a和b，则a²+a-b=.

查看试题解析
14. 一个三角形的两边长分别为2和3，第三边的长是方程x²-10x+21=0的根，则该三角形的第三边的长为

查看试题解析
15. 如果方程（x﹣1）（x²﹣2x+ $\frac{k}{4}$ ）＝0的三根可以作为一个三角形的三边之长，那么实数k的取值范围是．

查看试题解析

三、计算题

16. 解方程

(1)、用直接开平方法解 3（x-1）²-6＝0；

(2)、用配方法解x²-6x+3＝0；

(3)、用公式法解 9x²+10x＝4；

(4)、用因式分解法解 2x²-5x＝0．

查看试题解析
17. 解方程：

(1)、 $2 x^{2} - 3 x - 3 = 0 ($ 配方法 $)$

(2)、 $x^{2} - 2 x = 2 x + 1$ ；

(3)、 $(y - 2) (y - 3) = 12$ ；

(4)、 $(x - 1)^{2} - 3 (x - 1) + 2 = 0$ ．

查看试题解析

四、解答题

18. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + m - 1 = 0$ 有两个实数根．

(1)、求 $m$ 的取值范围；

(2)、设 $p$ 是方程的一个实数根，且满足 $(p^{2} - 2 p + 3) (m + 4) = 7$ ，求 $m$ 的值．

查看试题解析
19. 若x₁ ， x₂是一元二次方程2x²+4x-1＝0的两个根，求下列式子的值．

(1)、 $x_{1}^{2} + x_{2}^{2}$ ；

(2)、 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ．

查看试题解析
20.

(1)、已知关于 $x$ 的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 有两个实数根．
求证：无论 $m$ 取何值，方程总有两个实数根．

(2)、若▱ $A B C D$ 的两边 $A B$ ， $A D$ 的长是已知方程的两个实数根，当 $m$ 为何值时，▱ $A B C D$ 是菱形？求此菱形的边长．

查看试题解析
21. 某公园要在一个足够大的草地上规划出一个矩形草坪ABCD，矩形草坪ABCD的长AD为a米，宽AB为b米，并计划在草坪ABCD上种植两条宽均为x米的两条互相垂直的花带（阴影部分），且两条花带与矩形的边分别平行，余下的四块矩形草坪改为种植景观树．

(1)、已知 $a = 26$ ， $b = 15$ ，且种植景观树的总面积为312平方米，每条花带的宽为多少米？

(2)、若 $a ： b = 2 ： 1$ ，每条花带的宽均为2米，且种植景观树的总面积为312平方米，求a，b的值．

查看试题解析
22. 长白山之巅的天池是松花江、图们江、鸭绿江三江之源，夏融池水湛蓝：所以每年的七月和八月都会吸引大量游客前往观看 $.$ 今年 $7$ 月份，北坡游客接待中心平均每天每小时接待人数比西坡游客接待中心平均每天每小时接待人数多 $50 %$ ，两游客接待中心平均每天每小时接待游客共 $500$ 人．

(1)、求 $7$ 月份这两个游客接待中心平均每天每小时分别接待游客各多少人；

(2)、因为 $8$ 月份用天较多，游客减少，北坡游客接待中心平均每天每小时接待的人数比 $7$ 月少 $16 m$ 人，西坡游客接待中心平均每天每小时接待的人数比 $7$ 月少 $18 %$ ，在 $m$ 个小时内，这两个接待中心共接待 $1248$ 名游客，求 $m$ 的值．

查看试题解析
23. 世界杯火热进行期间，其相关的周边产品大多为中国制造 $.$ 为了抓住这一商机，两工厂决定生产球衣 $.$ 据统计，甲厂每小时生产 $600$ 件，乙厂每小时生产 $800$ 件 $.$ 甲、乙两厂共生产 $16$ 小时，且每天生产的球衣总数量为 $11400$ 件．

(1)、求甲、乙两厂每天分别生产多少小时？

(2)、由于球衣在国外热销，客户纷纷追加订单，两工厂每天均增加生产时间，其中甲厂比乙厂多增加 $2$ 小时，在整个生产过程中，甲厂每小时产量不变，而乙厂由于机器损耗及人员不足，每增加一个小时，每小时产量将减少 $140$ 件，这样两工厂一天生产的球衣总量将比原来多 $1200$ 件 $.$ 求甲厂增加的生产时间为多少小时？

查看试题解析