【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略5 图形的旋转
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 描述一个图形平移或旋转后正确的说法是( )A、图形形状与位置都不变 B、图形形状与大小都不变 C、图形形状与大小都变 D、图形形状与位置都变2. 美丽的冬奥雪花呈现出浪漫空灵的气质.如图,雪花图案是一个中心对称图形,也可以看成自身的一部分围绕它的中心依次旋转一定角度得到的,这个角的度数可以是( )
 A、 B、 C、 D、3. 下列图形绕某点旋转后,能与原来图形重合的是( )A、
A、 B、 C、 D、3. 下列图形绕某点旋转后,能与原来图形重合的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,∠AOB=90°,将Rt△AOB绕点O顺时针旋转20°得到△COD,则∠COB的度数是( )
4. 如图,∠AOB=90°,将Rt△AOB绕点O顺时针旋转20°得到△COD,则∠COB的度数是( ) A、20° B、70° C、90° D、110°5. 如图, 绕点 逆时针旋转90°到 的位置,已知 ,则 的度数为( )
A、20° B、70° C、90° D、110°5. 如图, 绕点 逆时针旋转90°到 的位置,已知 ,则 的度数为( ) A、55° B、35° C、40° D、45°6. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( )
A、55° B、35° C、40° D、45°6. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( ) A、 B、 C、 D、7. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到,点C在边EF上,过点E作AD平行线得矩形ANMD,则要知道矩形ANMD的面积只需知道( )
A、 B、 C、 D、7. 如图矩形ABCD由矩形EBGF逆时针旋转一个锐角得到,点C在边EF上,过点E作AD平行线得矩形ANMD,则要知道矩形ANMD的面积只需知道( ) A、S△BEC B、S△BGC C、S△ECM D、S△CGF8. 如图,是跷跷板的示意图,支柱OC与地面垂直,点O是AB的中点,AB绕着点O上下转动.当A端落地时,∠OAC=25°,则跷跷板上下可转动的最大角度(即∠A'OA)是( )
A、S△BEC B、S△BGC C、S△ECM D、S△CGF8. 如图,是跷跷板的示意图,支柱OC与地面垂直,点O是AB的中点,AB绕着点O上下转动.当A端落地时,∠OAC=25°,则跷跷板上下可转动的最大角度(即∠A'OA)是( ) A、25° B、35° C、45° D、50°9. 如图,在平面直角坐标系中,点是抛物线的图象的顶点,点 , 的坐标分别为 , , 将沿轴向下平移使点平移到点 , 再绕点逆时针旋转 , 若此时点 , 的对应点 , 恰好落在抛物线上,则的值为( )
A、25° B、35° C、45° D、50°9. 如图,在平面直角坐标系中,点是抛物线的图象的顶点,点 , 的坐标分别为 , , 将沿轴向下平移使点平移到点 , 再绕点逆时针旋转 , 若此时点 , 的对应点 , 恰好落在抛物线上,则的值为( )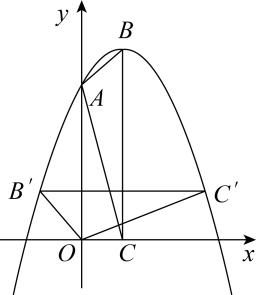 A、 B、-1 C、 D、-210. 如图,在平面直角坐标系中,已知点 , 点A在第一象限内, , , 将绕点О逆时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为( )
A、 B、-1 C、 D、-210. 如图,在平面直角坐标系中,已知点 , 点A在第一象限内, , , 将绕点О逆时针旋转,每次旋转90°,则第2023次旋转结束时,点A的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC= .
 12. 小明把一幅三角板按如图所示叠放在一起,固定三角板ABC,将另一块三角板DEF绕公共顶点B顺时针旋转(旋转的度数不超过180°).若二块三角板有一边平行,则三角板DEF旋转的度数可能是 .
12. 小明把一幅三角板按如图所示叠放在一起,固定三角板ABC,将另一块三角板DEF绕公共顶点B顺时针旋转(旋转的度数不超过180°).若二块三角板有一边平行,则三角板DEF旋转的度数可能是 .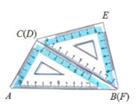 13. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是
13. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是 14. 如图,在中, , 把绕点逆时针旋转得到 , 连结CD,则CD的长为.
14. 如图,在中, , 把绕点逆时针旋转得到 , 连结CD,则CD的长为. 15. 如图,正方形ABCD与正方形AEFG边长分别为1和 , 一开始边AB与边AG重合,将正方形ABCD绕点A逆时针旋转,旋转角为 . 在旋转过程中,连接BG、GE、ED、DB,四边形BGED面积的最大值是 .
15. 如图,正方形ABCD与正方形AEFG边长分别为1和 , 一开始边AB与边AG重合,将正方形ABCD绕点A逆时针旋转,旋转角为 . 在旋转过程中,连接BG、GE、ED、DB,四边形BGED面积的最大值是 . 16. 太极推盘是一种常见的健身器材(如图1),转动两个圆盘便能锻炼身体.取推盘上半径均为0.4米的圆A与圆B(如图2)且AB=1米,圆A绕圆心A以2°每秒的速度逆时针旋转,圆B绕圆心B以2°每秒的速度顺时针旋转.开始转动时圆A上的点C恰好落在线段AB上,圆B上的点D在AB下方且满足∠DBA=60°,则在两圆同时开始转动的30秒内,CD的最小值是米.
16. 太极推盘是一种常见的健身器材(如图1),转动两个圆盘便能锻炼身体.取推盘上半径均为0.4米的圆A与圆B(如图2)且AB=1米,圆A绕圆心A以2°每秒的速度逆时针旋转,圆B绕圆心B以2°每秒的速度顺时针旋转.开始转动时圆A上的点C恰好落在线段AB上,圆B上的点D在AB下方且满足∠DBA=60°,则在两圆同时开始转动的30秒内,CD的最小值是米.
三、解答题
-
17. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1),(2,1),将△BOC绕点O逆时针旋转90度,得到△B1OC1 , 画出△B1OC1 , 并写出B、C两点的对应点B1、C1的坐标,
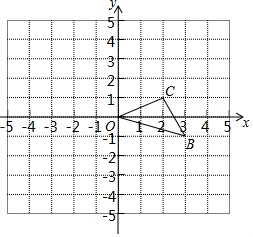 18. 如图所示,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC ,∠B=60°,求CD的长.
18. 如图所示,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC ,∠B=60°,求CD的长. 19. 如图, 中, ,在同一平面内,将 绕点 旋转到 的位置,使得 ,求 的度数
19. 如图, 中, ,在同一平面内,将 绕点 旋转到 的位置,使得 ,求 的度数 20. 在《几何原本》著作中,命题47:在直角三角形中,直角所对的边上的正方形等于夹直角两边上的正方形的和.古代人还没有发明勾股定理,他们如何证明这个命题是真命题.已知△ABC,∠BAC=90°;求证:以BC为边正方形的面积=以BA为边正方形的面积+以AC为边正方形的面积.
20. 在《几何原本》著作中,命题47:在直角三角形中,直角所对的边上的正方形等于夹直角两边上的正方形的和.古代人还没有发明勾股定理,他们如何证明这个命题是真命题.已知△ABC,∠BAC=90°;求证:以BC为边正方形的面积=以BA为边正方形的面积+以AC为边正方形的面积.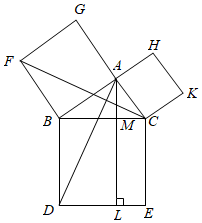 21. 如图,点 是等边 内一点, , ,将 绕点 按顺时针方向旋转 得 ,连接 .
21. 如图,点 是等边 内一点, , ,将 绕点 按顺时针方向旋转 得 ,连接 . (1)、求证: 是等边三角形;(2)、当 时,试判断 的形状,并说明理由.22. 如图①,在Rt△ABC中,∠B=90°,AB=5,BC=12,CD=5,DE∥AB.将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)、求证: 是等边三角形;(2)、当 时,试判断 的形状,并说明理由.22. 如图①,在Rt△ABC中,∠B=90°,AB=5,BC=12,CD=5,DE∥AB.将△EDC绕点C按顺时针方向旋转,记旋转角为α. (1)、①当α=0°时,=;②当α=180°时,= .(2)、试判断:当0≤α≤360°时,的大小有无变化?请仅就图②的情形给出证明.(3)、当△EDC旋转到A,D,E三点共线时,直接写出线段BD的长.23. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
(1)、①当α=0°时,=;②当α=180°时,= .(2)、试判断:当0≤α≤360°时,的大小有无变化?请仅就图②的情形给出证明.(3)、当△EDC旋转到A,D,E三点共线时,直接写出线段BD的长.23. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .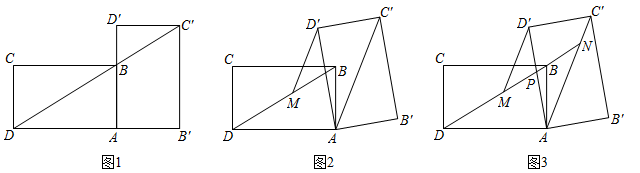
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.