【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略4 圆的认识
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 下列说法正确的是( ).A、弧是半圆 B、过圆心的线段是直径 C、直径是圆中最长的弦 D、半圆是圆中最长的弧2. 如图所示,四边形PAOB是扇形OMN的内接矩形,顶点在上,且不与点M,N重合.当点在上移动时,矩形PAOB的形状、大小随之变化,则AB的长( ).
 A、变大 B、变小 C、不变 D、无法判断3. 下列说法正确的有( )A、圆中最长的弦是直径 B、弦是直径 C、弧是半圆 D、圆只有一条对称轴4. 下列命题中,正确的个数是( )
A、变大 B、变小 C、不变 D、无法判断3. 下列说法正确的有( )A、圆中最长的弦是直径 B、弦是直径 C、弧是半圆 D、圆只有一条对称轴4. 下列命题中,正确的个数是( )①直径是弦,弦是直径;②弦是圆上的两点间的部分;③半圆是弧,但弧不一定是半圆;④直径相等的两个圆是等圆;⑤等于半径两倍的线段是直径.
A、2个 B、3个 C、4个 D、5个5. 如图,图中的弦共有( ) A、1条 B、2条 C、3条 D、4条6. 下列说法,正确的是( )A、半径相等的两个圆大小相等 B、长度相等的两条弧是等弧 C、直径不一定是圆中最长的弦 D、圆上两点之间的部分叫做弦7. 如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )
A、1条 B、2条 C、3条 D、4条6. 下列说法,正确的是( )A、半径相等的两个圆大小相等 B、长度相等的两条弧是等弧 C、直径不一定是圆中最长的弦 D、圆上两点之间的部分叫做弦7. 如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )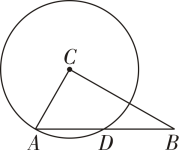 A、 B、3 C、9 D、68. 如图,、、是圆上的三点,且四边形是平行四边形,交圆于点 , 则等于( )
A、 B、3 C、9 D、68. 如图,、、是圆上的三点,且四边形是平行四边形,交圆于点 , 则等于( ) A、
A、
B、
C、
D、9. 如图,点A在数轴上表示的数是3,过点A作直线l垂直于OA , 在l上取点B , 使 , 以原点O为圆心,以OB为半径作弧,弧与数轴的交点C表示的数为( )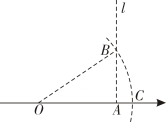 A、 B、 C、 D、10. 如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则 的最大值是( )
A、 B、 C、 D、10. 如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则 的最大值是( )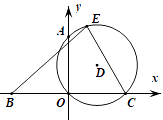 A、4 B、5 C、6 D、
A、4 B、5 C、6 D、二、填空题
-
11. 战国时期的数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,这句话中的“中”字的意思可以理解为12. 如图所示:点M、G、D在半圆O上,四边形OEDF、HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是bc(填<、=、>)
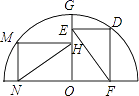 13. 某校计划在校园内修建一座周长为20m的花坛,同学们设计出正三角形,正方形和圆三种图案,通过计算说明使花坛面积最大的图案是 (填图形).14.
13. 某校计划在校园内修建一座周长为20m的花坛,同学们设计出正三角形,正方形和圆三种图案,通过计算说明使花坛面积最大的图案是 (填图形).14.如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是 °.
 15. 已知半径为R的半圆O,过直径AB上一点C,作CD⊥AB交半圆于点D,且CD=R,则AC的长为16. 过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为.
15. 已知半径为R的半圆O,过直径AB上一点C,作CD⊥AB交半圆于点D,且CD=R,则AC的长为16. 过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为.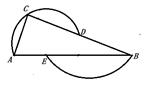
三、解答题
-
17. 一个圆形零件的部分碎片如图所示.请你利用尺规作图找到圆心O.(要求:不写作法,保留作图痕迹)
 18. 已知:如图,OA,OB是⊙O的两条半径,点C,D分别在OA,OB上,且AC=BD.求证:AD=BC.
18. 已知:如图,OA,OB是⊙O的两条半径,点C,D分别在OA,OB上,且AC=BD.求证:AD=BC. 19. 如图,AB为⊙O的直径,CD为⊙O的弦,AB,CD的延长线交于点E.若AB=2DE,∠E=16°,求∠AOC的度数.
19. 如图,AB为⊙O的直径,CD为⊙O的弦,AB,CD的延长线交于点E.若AB=2DE,∠E=16°,求∠AOC的度数. 20. 如图所示,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的函数表达式为为半圆的直径,求这个“果圆”被轴截得的CD的长.
20. 如图所示,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的函数表达式为为半圆的直径,求这个“果圆”被轴截得的CD的长. 21. 在平面直角坐标系xOy中,给出如下定义:将图形M绕直线x=3上某一点P顺时针旋转90°,得到图形M',再将图形M'关于直线x=3对称,得到图形N . 此时称图形N为图形M关于点P的“二次变换图形”.
21. 在平面直角坐标系xOy中,给出如下定义:将图形M绕直线x=3上某一点P顺时针旋转90°,得到图形M',再将图形M'关于直线x=3对称,得到图形N . 此时称图形N为图形M关于点P的“二次变换图形”.已知点A(0,1).
 (1)、若点P(3,0),直接写出点A关于点P的“二次变换图形”的坐标;(2)、若点A关于点P的“二次变换图形”与点A重合,求点P的坐标;(3)、若点P(3,-3),⊙O半径为1.已知长度为1的线段AB , 其关于点P的“二次变换图形”上的任意一点都在⊙O上或⊙O内,直接写出点B的纵坐标yB的取值范围.
(1)、若点P(3,0),直接写出点A关于点P的“二次变换图形”的坐标;(2)、若点A关于点P的“二次变换图形”与点A重合,求点P的坐标;(3)、若点P(3,-3),⊙O半径为1.已知长度为1的线段AB , 其关于点P的“二次变换图形”上的任意一点都在⊙O上或⊙O内,直接写出点B的纵坐标yB的取值范围.
