人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——第十一章综合测试
试卷更新日期:2023-12-12 类型:复习试卷
一、选择题
-
1. 在△ABC中,若∠A=∠B=∠C,则△ABC是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形2. 等腰三角形的两边长分别为6 cm和8 cm,则它的周长为( )A、20 cm B、22 cm C、20 cm或22 cm D、18 cm,20 cm或22 cm3. 下列长度的三条线段能组成三角形的是( )A、3,4,8 B、 , , C、4,5,9 D、4,5,84. 如图所示,点D在线段BC的延长线上,于点E,交AC于点F.如果 , , 则的度数为( )
 A、60° B、70° C、75° D、80°5. 如图,在△ABC中,M , N分别是边AB , BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( )
A、60° B、70° C、75° D、80°5. 如图,在△ABC中,M , N分别是边AB , BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( ) A、30° B、37° C、54° D、63°6. 如图,AD是△ABC的角平分线,E是AB的中点,△ABC的面积为21,AC=6,AB=8,则△BED的面积为( )
A、30° B、37° C、54° D、63°6. 如图,AD是△ABC的角平分线,E是AB的中点,△ABC的面积为21,AC=6,AB=8,则△BED的面积为( ) A、 B、5 C、6 D、7. 如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③DA平分∠CDE;④∠BDE=∠BAC;⑤S△ABD:S△ACD=AB:AC.其中结论正确的个数有( )
A、 B、5 C、6 D、7. 如图,∠C=90°,AD平分∠BAC,DE⊥AB于点E,有下列结论:①CD=ED;②AC+BE=AB;③DA平分∠CDE;④∠BDE=∠BAC;⑤S△ABD:S△ACD=AB:AC.其中结论正确的个数有( ) A、5个 B、4个 C、3个 D、2个8. 如图,已知 , , 点P是AB上的一点,连结CP , 将沿CP所在直线折叠,点A落在点M处,连结MB , MD . 若 , , 则( )
A、5个 B、4个 C、3个 D、2个8. 如图,已知 , , 点P是AB上的一点,连结CP , 将沿CP所在直线折叠,点A落在点M处,连结MB , MD . 若 , , 则( ) A、24° B、24.5° C、25° D、25.5°9. 如图,、、是五边形的三个外角,边、的延长线相交于点 , 如果 , 那么的度数为( )
A、24° B、24.5° C、25° D、25.5°9. 如图,、、是五边形的三个外角,边、的延长线相交于点 , 如果 , 那么的度数为( ) A、 B、 C、 D、10. 如图,点E、F为矩形ABCD边AD、AB上的一点,连接EB、EC、FD、FC,EB与DF、CF分别交于点和点M,EC与DF交于点 , 四边形AEPF的面积为的面积为的面积为 , 图中阴影部分的面积是( )
A、 B、 C、 D、10. 如图,点E、F为矩形ABCD边AD、AB上的一点,连接EB、EC、FD、FC,EB与DF、CF分别交于点和点M,EC与DF交于点 , 四边形AEPF的面积为的面积为的面积为 , 图中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知AD、DE、EF分别是△ABC、△ABD、△AED的中线,若S△ABC=24cm2 , 则阴影部分△DEF的面积为 .
 12. 如图,在中, , 和的平分线交于点 , 得 , 和的平分线交于点 , 得 , 则度.
12. 如图,在中, , 和的平分线交于点 , 得 , 和的平分线交于点 , 得 , 则度. 13. 如图,在△ABC中,∠ACB=90°,AC=BC , D为AB的中点,点M、N分别在AC、CB的延长线上,且MD⊥DN , 连MN . 若∠DMC=15°,BN=1,则MN的长是 .
13. 如图,在△ABC中,∠ACB=90°,AC=BC , D为AB的中点,点M、N分别在AC、CB的延长线上,且MD⊥DN , 连MN . 若∠DMC=15°,BN=1,则MN的长是 . 14. 如图,将△ABC沿CB边向右平移得到△DFE,DE交AB于点G.已知∠A:∠C:∠ABC=1:2:3,AB=9cm,BF=5cm,AG=5cm,则图中阴影部分的面积为 cm2 .
14. 如图,将△ABC沿CB边向右平移得到△DFE,DE交AB于点G.已知∠A:∠C:∠ABC=1:2:3,AB=9cm,BF=5cm,AG=5cm,则图中阴影部分的面积为 cm2 .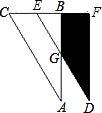 15. 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 海里.
15. 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 海里.
三、解答题
-
16. 如图,已知△ABC的两条高AD、CE相交于点O , ∠ACE=45°,∠DAC=20°,求∠B的度数.
 17. 如图,在△ABC中,AD是高线,AE、BF是角平分线,它们相交于点O , ∠BAC=50°,∠C=70°,求∠EAD与∠BOA的度数.
17. 如图,在△ABC中,AD是高线,AE、BF是角平分线,它们相交于点O , ∠BAC=50°,∠C=70°,求∠EAD与∠BOA的度数. 18. 如图,在△ABC中,BD,CE分别是∠ABC,∠ACB的平分线.
18. 如图,在△ABC中,BD,CE分别是∠ABC,∠ACB的平分线. (1)、若∠ABC=60°,∠ACB=40°,求∠BPC的度数.(2)、若∠A=80°,求∠BPC的度数.(3)、若∠A=x度,用含x的代数式表示∠BPC的度数.19.
(1)、若∠ABC=60°,∠ACB=40°,求∠BPC的度数.(2)、若∠A=80°,求∠BPC的度数.(3)、若∠A=x度,用含x的代数式表示∠BPC的度数.19.
在中,平分交于点 , 点是射线上的动点不与点重合 , 过点作交直线于点 , 的角平分线所在直线与射线交于点 .(1)、如图 , 点在线段上运动.
若 , , 则;
若 , 则°;(2)、探究与之间的数量关系,并说明理由;
(3)、若点在射线上运动时,与之间的数量关系与中的数量关系是否相同?若不同,请写出它们之间的数量关系并说明理由.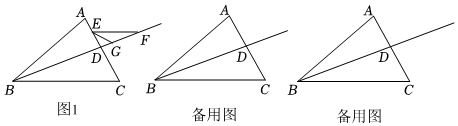 20. 已知的三边长分别为 , , .(1)、化简:;(2)、若 , , 且三角形的周长为偶数,求的值;
20. 已知的三边长分别为 , , .(1)、化简:;(2)、若 , , 且三角形的周长为偶数,求的值;