人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——11.3多边形及其内角和
试卷更新日期：2023-12-12 类型：复习试卷
一、选择题
-
1. 如图，将一个五边形ABCDE沿虚线裁去一个角后得到的多边形ABCDGF的内角和为（ ）
A、180° B、360° C、540° D、720°2. 如图，EC、BD是正五边形ABCDE的对角线，则∠1的大小为（ ）
A、72° B、75° C、60° D、80°3. 如图，小峰从点O出发，前进8m后向右转40°，再前进8m后又向右转40°，…，这样一直走下去，他第一次回到出发点O时，走的路程一共是（ ）m．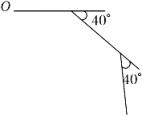
A、72 B、56 C、32 D、164. 如果一个多边形的边数增加2，那么关于其内角和与外角和的变化，下列说法正确的是（ ）A、内角和、外角和均增加 B、外角和不变，内角和增加 C、内角和不变，外角和增加 D、内角和、外角和均不变5. 从一个多边形的任何一个顶点出发都只有2条对角线，则它的边数是（ ）条.A、3 B、4 C、5 D、66. 若一个正n边形的内角和为720°，则它的每个外角度数是（ ）A、36° B、45° C、72° D、60°7. 下列命题：①各边相等的多边形是正多边形；②正多边形是轴对称图形；③正六边形的每个外角均为60°；④正n边形有（n-3）条对角线．其中真命题的个数为（ ）A、4 B、3 C、2 D、18. 若一个多边形截去一个角后，形成的新多边形的内角和是 ． 则原来多边形的边数可能是（ ）A、10或11 B、11 C、11或12 D、10或11或129. 如图，将透明直尺叠放在正五边形徽章ABCDE上，若直尺的下沿MN⊥DE于点O，且经过点B，上沿PQ经过点E，则∠ABM的度数为（ ）
A、152° B、126° C、120° D、108°10. 如图，把纸片沿折叠，当点落在四边形的外部时，此时测得 ， ， 则的度数为（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2＝度．
12. 图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消融，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5＝度．
13. 将正六边形与正方形按如图所示摆放，且正六边形的边AB与正方形的边CD在一条直线上，则∠BOC的度数是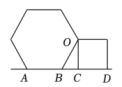
14. 如图，已知∠B+∠C＝150°，则∠A+∠D+∠E+∠F等于 （度）．
15. 一个多边形的内角和是外角和的4倍，则这个多边形的边数为三、解答题
-
16. 已知一个正多边形的边数为n ．(1)、若这个正多边形的一个内角为135°，求n的值．(2)、若这个多边形的内角和为其外角和的4倍，求n的值．17. 若一个多边形的内角和比它的外角和的倍多 ， 求这个多边形的边数和对角线的条数．18. 如图所示，根据图中的对话回答问题．
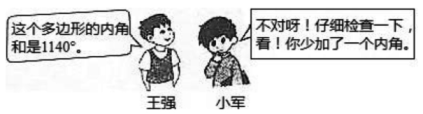(1)、王强是在求几边形的内角和？(2)、少加的那个内角为多少度？19. 某中学八年级数学课外兴趣小组在探究：“边形共有多少条对角线”这一问题时，设计了如下表格.请你完成探究过程并解决问题：
(1)、请在表格中的横线上填上相应的结果；多边形的边数
4
5
6
…
n
从多边形的一个顶点出发
1
2
…
多边形对角线的总条数
2
5
…
(2)、十边形有条对角线；(3)、过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为2023吗？若能，请求出这个多边形的边数；若不能，请说明理由.20. 如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中的变化情况，解答下列问题．
(1)、将下面的表格补充完整：正多边形的边数
的度数
(2)、根据规律，是否存在一个正边形，使其中的？若存在，直接写出的值；若不存在，请说明理由．(3)、根据规律，是否存在一个正边形，使其中的？若存在，直接写出的值；若不存在，请说明理由．
