人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——11.1与三角形有关的线段
试卷更新日期：2023-12-12 类型：复习试卷
一、选择题
-
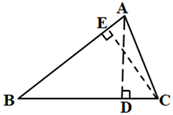
1. 等腰三角形一边长9cm，另一边长4cm， 它的第三边是（ ） cm．A、4 B、9 C、4或9 D、不能确定2. 如图，AD 是△ABC中∠BAC的平分线，DE⊥AB于点E，△ABC的面积为12，DE =2，AB = 7，则 AC 的长是（ ）
A、3 B、4 C、5 D、63. 如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样设计蕴含的数学依据是（ ）
A、两直线平行，内错角相等 B、垂线段最短 C、两点之间，线段最短 D、三角形具有稳定性4. 如图，△ABC中，D、E、F分别是AC、BD、AE的中点，如果S△DEF＝1cm2 ， 那么S△ABC＝（ ）cm2 ．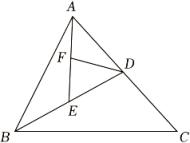
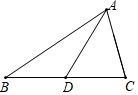
A、3 B、4 C、8 D、125. 如图，在△ABC中，AB=5，AC=9，AD是BC边上的中线，则AD的取值范围是（ ）
A、4<AD<14 B、0<AD<14 C、2<AD<7 D、5<AD<96. 若a、b、c为三角形的三边长，且a、b满足|a-2|+（b-1）2＝0，则第三边长c的值可以是（ ）A、1 B、2 C、3 D、47. 以下图示能表示△ABC的边BC上的高的是（ ）A、
B、
C、
D、
8. 下列说法中正确的个数是（ ）到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点
在角的内部到角两边距离相等的点在角的平分线上；
有两边和其中一边的对角分别相等的两个三角形不一定全等；
等腰三角形的角平分线，中线，高线互相重合，简称三线合一．A、 B、 C、 D、9. 已知为的中线，且 ， ， 则与的周长之差为（ ）A、 B、 C、 D、10. 已知a，b，c是三角形的三条边，则的化简结果为（ ）A、0 B、 C、 D、二、填空题
-
11. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E ， S△ABC＝24，DE＝4，AB＝5，则AC的长是 ．
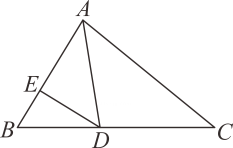12. 长分别为11，8，6，4的四根木条，选其中三根组成三角形种选法．13. 已知BD是△ABC的中线，若△ABD与△BCD的周长分别为21，12，则AB-BC=14. 桥梁搭桥，电视塔底座都是三角形结构，这是利用三角形的性．15. 一个三角形的三边长分别是：3，5， ， 则的取值范围为.三、解答题
-
16. 如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数．
17. 已知的三边长是 ， ， ．(1)、若 ， ， 且三角形的周长是小于的偶数求边的长；(2)、化简 ．18. 如图，在6×10的网格中，每一小格均为正方形且边长是1，已知△ABC的每个顶点都在格点上。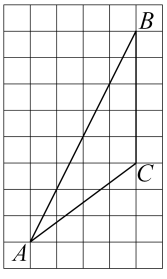
(1)、画出△ABC中BC边上的高线AE；(2)、在△ABC中AB边上取点D ， 连接CD ， 使S△BCD＝3S△ACD；(3)、直接写出△BCD的面积是 ．19. 如图，在中， ． ， 是的高，点E在边上，且是的角平分线，// ， 求和的度数．
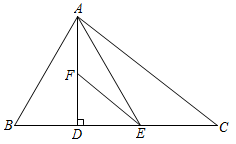20. 如图，AD为△ABC的中线，AB = 12cm，△ABD和△ADC的周长差是4cm，求△ABC的边AC的长(AC AB).
