【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略3 概率

试卷更新日期：2023-12-11 类型：复习试卷

进入 出卷网 下载

一、选择题

  • 1. 下列选项中的事件，属于随机事件的是（    ）
    A、任意选择某一电视频道，它正在播放广告 B、人在月球上所受重力比在地球上小 C、在一个只有白球的袋中，摸出白球 D、两个负数相加和是负数

    查看试题解析

  • 2. 连续掷两枚质地均匀的硬币，出现一枚正面朝上、一枚反面朝上的概率为（  ）
    A、12 B、13 C、14 D、1

    查看试题解析

  • 3. 从1~9这几个自然数中任取一个，是2的倍数或是3的倍数的概率是（ ）
    A、19 B、29 C、23 D、59

    查看试题解析

  • 4. 某年度男子职业联赛整个常规赛季中，某球员罚球投篮的命中率大约是83.3%．下列说法错误的是（ ）．
    A、该球员罚球投篮2次，一定全部命中 B、该球员罚球投篮2次，不一定全部命中 C、该球员罚球投篮1次，命中的可能性较大 D、该球员罚球投篮1次，不命中的可能性较小

    查看试题解析

  • 5. 下列说法正确的是（ ）
    A、“打开电视，正在播放本溪新闻节目”是必然事件 B、某种彩票中奖率为10%是指买十张一定有一张中奖 C、“明天降雨的概率是50%”表示明天有半天都在降雨 D、“掷一次骰子，向上一面的点数是6”是随机事件

    查看试题解析

  • 6. 在如图所示的图形中，每个三角形上各有一个数字，若六个三角形上的数字之和为20，则称该图形是“和谐图形”，已知其中四个三角形上的数字之和为14，现从1，2，3，4，5中任取两个数字标在另外两个三角形上，则恰好使该图形为“和谐图形”的概率为（ ）.

    A、310 B、15 C、110 D、320

    查看试题解析

  • 7. 不透明的口袋中装有3个黄球、1个红球和n个蓝球，这些小球除颜色外其余均相同，课外兴趣小组每次摸出一个球记录下颜色后再放回，大量重复试验后发现，摸到蓝球的频率稳定在0.6，则n的值最可能是（  ）
    A、4 B、5 C、6 D、7

    查看试题解析

  • 8. 如图，电路图上有1个电源，4个开关和1个完好的小灯泡，随机闭合2个开关，则小灯泡发光的概率为（ ）

    A、16 B、23 C、14 D、13

    查看试题解析

  • 9. 甲乙丙丁四人互相给其他三人之一写信，选择对象的方式等可能.问存在两个人收到对方的信的概率（   ）
    A、23 B、59 C、1727 D、5581

    查看试题解析

  • 10. 一个密码锁有五位数字组成，每一位数字都是0，1，2，3，4，5，6，7，8，9之中的一个，小明只记得其中的三个数字，则他一次就能打开锁的概率为（   ）
    A、15 B、12 C、120 D、1100

    查看试题解析

二、填空题

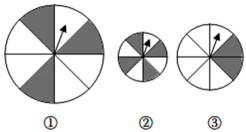
  • 11. 打开电视机，正在转播《非遗里的中国》（一档节目），这个事件是事件．（填“必然”“不可能”或“随机”）

    查看试题解析

  • 12. 如图，转动三个可以自由转动的转盘（转盘均被等分），当转盘停止转动后，根据“指针落在灰色区域内”的可能性的大小，将转盘的序号按事件发生的可能性从大到小排列为 ．

    查看试题解析

  • 13. 如图，甲、乙、丙3人站在5×5网格中的三个格子中，小王随机站在剩下的空格中，与图中3人均不在同一行或同一列的概率是 ．

    查看试题解析

  • 14. 如图，矩形ABCD中，AB=2，BC=4，E为BC的中点，连接AE、DE．以E为圆心，BE长为半径画弧，分别与AE，DE交于点F，G．向该矩形ABCD游戏板随机发射一枚飞针，则击中图中阴影部分区域的概率为  ．

    查看试题解析

  • 15. 小明向如图所示的圆形区域内投掷飞镖.已知△ABC是等边三角形，D点是弧AC的中点，则飞镖落在阴影部分的概率为.

    查看试题解析

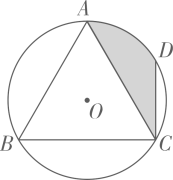  • 16. 某学校举行文学知识大赛，每场比赛都有编号为1~10号共10道测试题供选手随机抽取作答．在某场比赛中，前两位选手已分别抽走了6号、9号题，第3位选手抽中3号题的概率是

    查看试题解析

三、解答题

  • 17. 某校元旦晚会设立了抽奖活动，共准备150张奖券，设特等奖1个，一等奖15个，二等奖30个，三等奖50个．已知每张奖券获奖的可能性相同．求：
    (1)、一张奖券中特等奖的概率．
    (2)、一张奖券中奖的概率．
    (3)、一张奖券中一等奖或二等奖的概率．

    查看试题解析

  • 18. 某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被平均分成16份），如图所示．并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会，转盘停止后，指针正好对准哪个区域，顾客就可以获得相应的奖品．小红和妈妈购买了168元的商品，请你分析计算：

    颜色

    奖品

    红色

    玩具熊

    黄色

    童话书

    绿色

    彩笔

    (1)、小红获得童话书的概率是多少？
    (2)、小红获得奖品的概率是多少？

    查看试题解析

  • 19. 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：

    摸球的

    次数n

    100

    200

    300

    500

    800

    1 000

    3 000

    摸到白球

    的次数m

    70

    128

    171

    302

    481

    599

    1 806

    摸到白球

    的频率mn

    0.7

    0.64

    0.57

    0.604

    0.601

    0.599

    0.602

    (1)、请估计当n很大时，摸到白球的概率为(精确到0.1).
    (2)、估算盒子里有白球个. 
    (3)、若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在 0.5，那么可以推测出x最有可能是多少?

    查看试题解析

  • 20. 2021年，成都将举办世界大学生运动会，这是在中国西部第一次举办的世界综合性运动会．目前，运动会相关准备工作正在有序进行，比赛项目已经确定．某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿，并根据调查结果绘制成了如图两幅不完整的统计图．

    根据以上信息，解答下列问题：

    (1)、这次被调查的同学共有人；
    (2)、扇形统计图中“篮球”对应的扇形圆心角的度数为；
    (3)、现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者，请利用画树状图或列表的方法，求恰好选中甲、乙两位同学的概率．

    查看试题解析

  • 21. 端午节历来有吃粽子的习俗．某公司为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A，B，C，D表示)这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图(尚不完整)．

    请根据以上信息回答：

    (1)、本次参加抽样调查的居民有多少人？将两幅不完整的图补充完整．
    (2)、若居民区有10000人，估计爱吃D粽的人数．
    (3)、若有外形完全相同的A，B，C，D粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．

    查看试题解析

  • 22. 图为国家节水标志，节水标志各部分的含义为：灰色的圆形代表地球，标志留白部分像一只手托起一滴水，手又像一条蜿蜒的河流，象征滴水汇成江河．某市在实施居民用水定额管理前，对居民生活用水情况进行了调查，通过简单随机抽样调查获得了50个家庭去年的月均用水量（单位：吨）．以下是整理数据后的不完整统计表、统计图．

        

                                                                                                                                                                                                                                                                               

    月均用水量频数分布表

    分组

    频数

             2≤x<3

    4

             3≤x<4

    12

             4≤x<5

             a

             5≤x<6

    9

             6≤x<7

    5

             7≤x<8

    4

             8≤x<9

    2

    合计

    50

        
      请根据图表中提供的信息解答下列问题：

    (1)、表中a的值为 ， 请补全频数分布直方图；
    (2)、扇形统计图中，月均用水量为“E：6≤x<7”的扇形的圆心角是°；
    (3)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费．若要使60%的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？为什么？

    查看试题解析

  • 23. 某化妆品专卖店，为了吸引顾客，在“母亲节”当天举办了某种品牌化妆品有奖酬宾活动，凡购物满188元者，有两种奖励方案供选择：第一种方案是直接获得18元的礼金券，第二种方案是得到一次摇奖的机会．已知在摇奖机内装有2个红球和2个白球，除颜色外其它都相同，摇奖者必须从摇奖机内一次连续摇出两个球，根据球的颜色决定送礼金券的多少（如表）

    某种品牌化妆品

    球

    两红

    一红一白

    两白

    礼金券（元）

    12

    24

    12

    (1)、请你用列表法（或画树状图法）求一次连续摇出一红一白两球的概率．
    (2)、如果一名顾客当天在本店购物满188元，若只考虑获得最多的礼品券，请你帮助分析选择哪种方案较为实惠．

    查看试题解析