浙教版数学七年级上册期末冲刺满分攻略3 绝对值

试卷更新日期：2023-12-11 类型：复习试卷

进入出卷网下载

一、选择题

1. 若 $| x | = 2 ， | y | = 3$ ，且 $x y < 0$ ，则 $x + y$ 的值是（）

A、1 B、5 C、-1或1 D、5或-5

查看试题解析
2. 有理数a，b，c在数轴上的对应点的位置如图所示.若 $| a | > | b | ， | c | > | b |$ ，则下列络论不一定成立的是（）

A、 $a < 0$ B、 $c > 0$ C、 $a + b < 0$ D、 $a + c < 0$

查看试题解析
3. 已知a，b满足|a+3|+（b-2）²＝0，则a+b的值为（　　）

A、1 B、5 C、-1 D、-5

查看试题解析
4. 已知： $m = \frac{| a + b |}{c} + \frac{2 | b + c |}{a} + \frac{3 | c + a |}{b}$ ，且 $a b c > 0$ ， $a + b + c = 0 .$ 则 $m$ 共有 $x$ 个不同的值，若在这些不同的 $m$ 值中，最大的值为 $y$ ，则 $x + y =$ （）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
5. 已知 $| x - 2 | + {(y + 8)}^{2} = 0$ ，则 $x + y$ 的值为（）

A、10 B、不能确定 C、-6 D、-10

查看试题解析
6. 有理数满足a+b<0，|a+b|=|a|-|b|，则下列结论正确的是（）

A、a<b<0 B、a>b>0 C、a<0<b D、b<a<0

查看试题解析
7. 现有30个数，其中所有正数之和为10，负数之和为 $a$ ，这30个数的绝对值之和为（）

A、 $10 + a$ B、 $20 + a$ C、 $10 - a$ D、 $20 - a$

查看试题解析
8. 已知a＝- $\frac{3}{400}$ ， b＝ $\frac{7}{300}$ ， c＝- $\frac{11}{200}$ ，则下列各式结果最大的是（）

A、|a+b+c| B、|a+b-c| C、|a-b+c| D、|a-b-c|

查看试题解析
9. 有理数a，b在数轴上对应的位置如图所示，那么代数式 $\frac{| a + 1 |}{a + 1} - \frac{| a |}{a} + \frac{b - a}{| a - b |} - \frac{1 - b}{| b - 1 |}$ 的值是（）

A、- 1 B、0 C、1 D、2

查看试题解析
10. 实数 $x ， y ， z$ 在数轴上的对应点的位置如图所示，若 $| z + y | < | x + y |$ ，则A，B，C，D四个点中可能是原点的为（）

A、A点 B、B点 C、C点 D、D点

查看试题解析

二、填空题

11. 已知 $| a | = 9 ， | b | = 3$ ，则 $| a - b | = b - a$ ，则 $a + b$ 的值．

查看试题解析
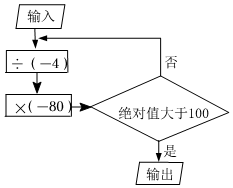
12. 已知 $| x | = 6$ ， $y = - 2$ ，且 $| x - y | = x - y$ ，则 $x - y =$ .

查看试题解析
13. 整数a、b、c满足1000|a|+10|b|+|c|=2023，其中|a|>1且abc>1，则a+b+c的最小值是．

查看试题解析
14. 小海在自学了简单的电脑编程后，设计了如图所示的程序，若他输入的数是-2，则执行了程序后，输出的数是.

查看试题解析
15. 已知|a|＝5，|b|＝3，若|a+b|＝a+b，则a+b＝．

查看试题解析
16. 对于有理数 $a$ ， $b$ ， $n$ ，若 $| a - n | + | b - n | = 1$ ，则称 $b$ 是 $a$ 关于 $n$ 的“相关数”，例如， $| 2 - 2 | + | 3 - 2 | = 1$ ，则3是2关于2的“相关数”．若 $x_{1}$ 是 $x$ 关于1的“相关数”， $x_{2}$ 是 $x_{1}$ 关于2的“相关数”，…， $x_{4}$ 是 $x_{3}$ 关于4的“相关数”．则 $x_{1} + x_{2} + x_{3} =$ ．（用含 $x$ 的式子表示）

查看试题解析

三、解答题

17. 计算：

(1)、 $- 2^{2} \times \frac{1}{4} + 4 \div \frac{4}{9} + (- 1)^{2023}$ ；

(2)、 $- 1^{4} + | 2 - (- 3)^{2} |$ $+ \frac{1}{2} \div (- \frac{3}{2})$ .

查看试题解析
18. 化简求值：（5x²y+5xy﹣7x）﹣ $\frac{1}{2}$ （4x²y+10xy﹣14x），其中x，y满足 ${(x - 1)}^{2} + | y + 2 | = 0$ 。

查看试题解析
19. 数轴是一个非常重要的数学工具，实数和数轴上的点能建立一一对应的关系，它建立了数与形的联系，是初中“数形结合”的基础。我们知道一个数在数轴上对应的点到原点的距离叫做这个数的绝对值，如： $| - 3 | = 3$ ， $| x |$ ：表示数 $x$ 的点到原点的距离。同样的， $| x - 3 |$ ：表示数 $x$ 的点到表示数3的点的距离。请结合数轴解决下列问题：

①当 $x = 5$ 时， $| x - 3 |$ 表示什么意思？；

②若 $| x - 3 | = 5$ ，则 $x =$ ；

③若 $| x - 2 | + | x + 3 | = 7$ ，则 $x$ 的值是；

④求使 $| x - 4 | + | x + 1 |$ 的值最小的所有符合条件的整数 $x$ .

查看试题解析
20. 某市今年受台风“梅花”的影响，在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从 $A$ 地出发，晚上到达 $B$ 地，约定向东为正方向，当天的航行路程记录如下 $（$ 单位：千米 $）$ ：
$+ 14$ ， $- 10$ ， $+ 8$ ， $- 7$ ， $+ 11$ ， $- 6$ ， $+ 9$ ， $- 5$ ．

(1)、请你帮忙确定 $B$ 地位于 $A$ 地的什么方向，距离 $A$ 地多少千米的地方？

(2)、若冲锋舟每千米耗油 $0.6$ 升，油箱容量为 $30$ 升，求冲锋舟当天救灾过程中至少还需补充多少升油？

查看试题解析
21. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上对应点的位置如图所示.
解答下列各题：

(1)、判断下列各式的符号： $① c$ $0$ ； $② | a |$ $| c |$ ； $($ 填“ $>$ ”、“ $<$ ”或“ $=$ ” $)$

(2)、化简： $| a - b | + | b - c | - | c - a | + | b + c |$ .

查看试题解析
22. 若数轴上的点A、点B表示的数分别为 $a ， b$ ，则A、B两点之间的距离AB＝|a-b|，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．
解决问题：现数轴上有一点A表示的数为-10，点B表示的数为18，点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒（t＞0）．

(1)、①A、B两点之间的距离AB＝，线段AB的中点表示的数为． ②当t＝时，P、Q两点相遇，相遇点所表示的数为．

(2)、求当t为何值时，PQ＝ $\frac{1}{2}$ AB．

(3)、折叠数轴使点A、P重合，折点记为M，还原后再折叠数轴使点B、P重合，折点记为N，点P在运动过程中，M、N两点间的距离是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长度．

查看试题解析
23. 同学们都知道： $∣ 3 - (- 2)$ |表示3与-2之差的绝对值，实际上也可理解为3与-2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索：

(1)、数轴上表示 $x$ 与3的两点之间的距离可以表示为.

(2)、如果 $| x - 3 | = 5$ ，则 $x =$ .

(3)、同理 $| x + 2 | + | x - 1 |$ 表示数轴上有理数 $x$ 所对应的点到-2和1所对应的点的距离之和，请你找出所有符合条件的整数 $x$ ，使得 $| x + 2 | + | x - 1 | = 3$ .

(4)、由以上探索猜想对于有理数 $x ， | x + 3 | + | x - 6 |$ 是否有最小值?如果有，直接写出最小值；如果没有，说明理由.

查看试题解析
24. 如图，数轴上的点从左往右依次A，B，C对应的数分别为a，b，c，且|a+3|+|b-6|=0，AB的距离比BC的距离大4，动点P从点A出发沿数轴以每秒6个单位的速度向右运动，同时动点Q从点B出发沿数轴以每秒2个单位的速度一直向右运动，当点P运动到点C之后立即以原速沿数轴一直向左运动，设运动的时间为t秒.

(1)、填空：a＝， b＝，点Q在数轴上所表示的数为（用含t的代数式表示）.

(2)、当动点P从点A运动到点C过程中，Q点是PC的中点时，则点Q在数轴上所表示的数是多少？

(3)、在整个运动过程中，是否存在t使得QB=2PC，若存在，求出t的值，若不存在，请说明理由.

查看试题解析