【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略2 二次函数的应用

试卷更新日期：2023-12-11 类型：复习试卷

进入出卷网下载

一、选择题

1. 关于二次函数y=-（x-3）²+2的最值，下列说法正确的是（）

A、有最大值3 B、有最小值3 C、有最大值2 D、有最小值2

查看试题解析
2. 观察下面的表格，一元二次方程 $x^{2} - x = 1.4$ 的一个近似解是（）
$x$
$1.1$
$1.2$
$1.3$
$1.4$
$1.5$
$1.6$
$1.7$
$1.8$
$1.9$
$x^{2} - x$
$0.11$
$0.24$
$0.39$
$0.56$
$0.75$
$0.96$
$1.19$
$1.44$
$1.71$

A、 $0.11$ B、 $1.6$ C、 $1.7$ D、 $1.8$

查看试题解析
3. 二次函数y＝ax²-2ax+c（a≠0）的图象过点（3，0），方程ax²-2ax+c＝0的解为（）

A、x₁＝-3，x₂＝-1 B、x₁＝-1，x₂＝3 C、x₁＝1，x₂＝3 D、x₁＝-3，x₂＝1

查看试题解析
4. 现有一根长为50cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm ² ，一边长为xcm，则y与x之间的函数表达式为（）

A、y=x(50-x) B、y=x(50-2x) C、y=x(25-2x) D、y=x(25-x)

查看试题解析
5. 已知抛物线 $y = a x^{2} + b x + c$ 与x轴有两个不同的交点，则关于x的一元二次方程 $a x^{2} + b x + c = 0$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、实数根 D、无法确定

查看试题解析
6. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）

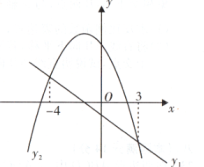A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析
7. 已知抛物线y=x²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是（）

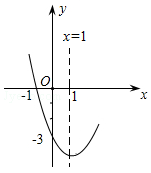A、x＜-1 B、-1＜x＜3 C、x＜-1或x＞3 D、x＜-1或x＞4

查看试题解析
8. 如图，抛物线 $y = x^{2} - 2 x - 3$ 与 $y$ 轴交于点 $C$ ，点 $D$ 的坐标为 $(0 ， - 1)$ ，在第四象限抛物线上有一点 $P$ ，若 $△ P C D$ 是以 $C D$ 为底边的等腰三角形，则点 $P$ 的横坐标为（）

A、 $1 + \sqrt{2}$ B、 $1 - \sqrt{2}$ C、 $\sqrt{2} - 1$ D、 $1 - \sqrt{2}$ 或 $1 + \sqrt{2}$

查看试题解析
9. “抖音直播带货”已经成为一种热门的销售方式，某抖音主播代销某一品牌的电子产品（这里代销指厂家先免费提供货源，待货物销售后再进行结算，未售出的由厂家负责处理）．销售中发现每件售价99元时，日销售量为200件，当每件电子产品每下降5元时，日销售量会增加10件．已知每售出1件电子产品，该主播需支付厂家和其他费用共50元，设每件电子产品售价为x（元），主播每天的利润为w（元），则w与x之间的函数解析式为（）

A、 $w = (99 - x) [200 + 10 (x - 50)]$ B、 $w = (x - 50) [200 + 10 (99 - x)]$ C、 $w = (x - 50) (200 + \frac{x - 99}{5} \times 10)$ D、 $w = (x - 50) (200 + \frac{99 - x}{5} \times 10)$

查看试题解析
10. 如图，已知抛物线经过点 $B (- 1 ， 0)$ ， $A (4 ， 0)$ ，与y轴交于点 $C (0 ， 2)$ ， P为AC上的一个动点，则有以下结论：①抛物线的对称轴为直线 $x = \frac{3}{2}$ ；②抛物线的最大值为 $\frac{9}{8}$ ；③ $∠ A C B = 90 °$ ；④OP的最小值为 $\frac{4 \sqrt{5}}{5}$ ．则正确的结论为（）

A、①②④ B、①② C、①②③ D、①③④

查看试题解析

二、填空题

11. 某工厂今年八月份医用防护服的产量是50万件，计划九月份和十月份增加产量，如果月平均增长率为x，那么十月份医用防护服的产量y（万件）与x之间的函数表达式为．

查看试题解析
12. 已知二次函数 $y = a x^{2} - 4 a x + 8 (a \neq 0)$ 的图象与 $x$ 轴交于 $A ， B$ 两点．若 $A B = 6$ ，则 $a =$ ．

查看试题解析
13. 某产品每件成本10元，试销阶段每件产品的销售单价x（元/件）与日销售量y（件）之间的关系如下表．
x（元∕件）
15
18
20
22
…
y（件）
250
220
200
180
…
按照这样的规律可得，日销售利润w（元）与销售单价x（元/件）之间的函数关系式是．

查看试题解析
14. 要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 $1 m$ 处达到最高，高度为 $3 m$ ，水柱落地处离池中心 $3 m$ ，水管长度应为．

查看试题解析
15. 开口向上的抛物线 $y = a x^{2} - 2 a x - 1$ 过点 $(- 1 ， y_{1})$ ， $(1 ， y_{2})$ ， $(4 ， y_{3})$ ，若 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 三个数中有且只有一个数大于零，则a的取值范围是.

查看试题解析
16. 如图1，在 $▱ A B C D$ 中， $∠ B = 60 ° ， B C = 2 A B$ ，动点 $E$ 从点 $A$ 出发，以每秒1个单位的速度沿线段 $A B$ 运动到点 $B$ 停止，同时动点 $F$ 从点 $B$ 出发，以每秒4个单位的速度沿折线 $B - C - D$ 运动到点 $D$ 停止．图2是点 $E ， F$ 运动时， $△ B E F$ 的面积 $S$ 与运动时间 $t$ 函数关系的图象，则 $a$ 的值是．

查看试题解析

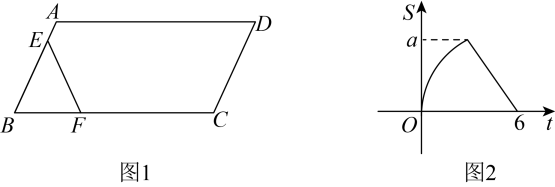
三、解答题

17. 已知抛物线的对称轴是直线x=2，顶点在直线y=x-1上，并且经过点(3，-8)．

(1)、求这条抛物线的函数表达式；

(2)、若点(1，y₁)和(4，y₂)都在这条抛物线上，试判断y₁、y₂的大小关系．

查看试题解析
18. 已知二次函数y＝x²＋2(m－1)x－2m（m为常数）．

(1)、求证无论m为何值，该函数图象与x轴总有两个公共点；

(2)、若点A(x₁ ，－1)､B(x₂ ，－1)在该函数图象上，将图像沿直线AB翻折，顶点恰好落在x轴上，求m的值．

查看试题解析
19. 用10米的铝合金制成如图窗框矩形ABCD，其中点E，F分别在边AB，CD上，点G，H分别在边EF，BC上，且EF∥BC，GH⊥BC，BE=BC，BE≥3AE，记窗框矩形ABCD的面积为s平方米，边长BC为x米．

(1)、求s关于x的表达式及自变量x的取值范围．

(2)、求s的最大值．

查看试题解析
20. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行，大熊猫是成都最具特色的对外传播标识物和“品牌图腾”，是天府之国享有极高知名度的个性名片．此次成都大运会吉祥物“蓉宝”（如图1）便是以熊猫基地真实的大熊猫“芝麻”为原型创作的．某商店销售“蓉宝”的公仔毛绒玩具，进价为30元/件，经市场调查发现：该商品的月销售量y（件）与销售价x（元/件）之间的关系如图2所示．
图1 图2

(1)、求y关于x的函数解析式；

(2)、由于某种原因，该商品进价提高了a元/件（ $a > 0$ ），如果规定该玩具售价不超过40元/件，该商品在今后的销售中，月销售量与销售价仍然满足（1）中的函数关系，若该商品的月销售最大利润是2400元，求a的值．

查看试题解析
21. 小明在一次打篮球时，篮球传出后的运动路线为如图所示的抛物线，以小明所站立的位置为原点 $O$ 建立平面直角坐标系，篮球出手时在 $O$ 点正上方 $1 m$ 处的点 $P .$ 已知篮球运动时的高度 $y (m)$ 与水平距离 $x (m)$ 之间满足函数表达式 $y = - \frac{1}{8} x^{2} + x + c$ ．

(1)、求 $y$ 与 $x$ 之间的函数表达式；

(2)、求篮球在运动的过程中离地面的最大高度；

(3)、小亮手举过头顶，跳起后的最大高度为 $B C = 2.5 m$ ，若小亮要在篮球下落过程中接到球，求小亮离小明的最短距离 $O B$ ．

查看试题解析
22. 如图，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与坐标轴相交于 $A (0 ， - 2)$ ， $B (4 ， 0)$ 两点，点D为直线 $A B$ 下方抛物线上一动点，过点D作x轴的垂线，垂足为G； $D G$ 交直线 $A B$ 于点E．

(1)、求抛物线的函数表达式；

(2)、求 $E D$ 的最大值；

(3)、过点B的直线 $y = - 2 x + 8$ 交y轴于点C，交直线 $D G$ 于点F，H是y轴上一点，当四边形 $B E H F$ 是矩形时，求点H的坐标．

查看试题解析
23. 某公园修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安装一个可调节角度的喷水头，从喷水头喷出的水柱形状是一条抛物线．建立如图所示的平面直角坐标系，抛物线形水柱的竖直高度 $y$ （单位：m）与到池中心的水平距离 $x$ （单位：m）满足的关系式近似为 $y = a {(x - h)}^{2} + k$ （ $a < 0$ ）．

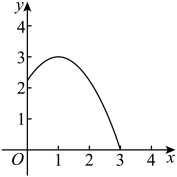(1)、在某次安装调试过程中，测得 $x$ 与 $y$ 的部分对应值如下表：
水平距离 $x / m$
0
0.5
1
1.5
2
2.5
3
竖直高度 $y / m$
2.25
2.8125
3
2.8125
2.25
1.3125
0
根据表格中的数据，解答下列问题：
①水管的长度是m；
②求出 $y$ 与 $x$ 满足的函数解析式 $y = a {(x - h)}^{2} + k$ （ $a < 0$ ）；

(2)、安装工人在上述基础上进行了下面两种调试：
①不改变喷水头的角度，将水管长度增加1m，水柱落地时与池中心的距离为 $d_{1}$ ；
②不改变水管的长度，调节喷水头的角度，使得水柱满足 $y = - 0.6 {(x - 1.5)}^{2} + 3.6$ ，水柱落地时与池中心的距离为 $d_{2}$ ．则比较 $d_{1}$ 与 $d_{2}$ 的大小关系是： $d_{1}$ $d_{2}$ （填“ $>$ ”或“ $=$ ”或“ $<$ ”）

查看试题解析

$x$	$1.1$	$1.2$	$1.3$	$1.4$	$1.5$	$1.6$	$1.7$	$1.8$	$1.9$
$x^{2} - x$	$0.11$	$0.24$	$0.39$	$0.56$	$0.75$	$0.96$	$1.19$	$1.44$	$1.71$

水平距离 $x / m$	0	0.5	1	1.5	2	2.5	3
竖直高度 $y / m$	2.25	2.8125	3	2.8125	2.25	1.3125	0

x（元∕件）	15	18	20	22	…
y（件）	250	220	200	180	…