【北师大版】2023-2024学年数学八年级(上)期末仿真模拟试题(一)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 点关于y轴对称的点的坐标是( )A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )A、 B、 C、9 D、63. 如图,估计的值所对应的点可能落在( )
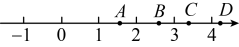 A、点A处 B、点B处 C、点C处 D、点D处4. 直线和相交于x轴上同一点,则的值为
A、点A处 B、点B处 C、点C处 D、点D处4. 直线和相交于x轴上同一点,则的值为 ( ) A、 B、 C、3 D、-35. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
( ) A、 B、 C、3 D、-35. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( ) A、 B、 C、 D、6. 小明在计算一组数据的方差时,列出的公式如下 ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是7. 在下列条件中:①;②;③;④ , 能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个8. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、
A、 B、 C、 D、6. 小明在计算一组数据的方差时,列出的公式如下 ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是7. 在下列条件中:①;②;③;④ , 能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个8. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、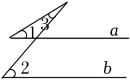 B、
B、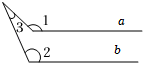 C、
C、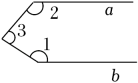 D、
D、 9. 甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( )
9. 甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( ) A、甲的射击成绩比乙的射击成绩更稳定 B、甲射击成绩的众数大于乙射击成绩的众数 C、甲射击成绩的平均数大于乙射击成绩的平均数 D、甲射击成绩的中位数大于乙射击成绩的中位数10. 为了研究吸烟对肺癌是否有影响,某研究机构随机调查了8000人,结果显示:在吸烟者中患肺癌的比例是3%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多33人.在这8000人中,设吸烟者患肺癌的人数为x , 不吸烟者患肺癌的人数为y . 所列方程组正确的是( )A、 B、 C、 D、
A、甲的射击成绩比乙的射击成绩更稳定 B、甲射击成绩的众数大于乙射击成绩的众数 C、甲射击成绩的平均数大于乙射击成绩的平均数 D、甲射击成绩的中位数大于乙射击成绩的中位数10. 为了研究吸烟对肺癌是否有影响,某研究机构随机调查了8000人,结果显示:在吸烟者中患肺癌的比例是3%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多33人.在这8000人中,设吸烟者患肺癌的人数为x , 不吸烟者患肺癌的人数为y . 所列方程组正确的是( )A、 B、 C、 D、二、填空题(每题3分,共15分)
-
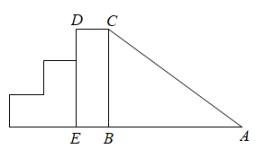
11. 命题“内错角相等,两直线平行”的条件是.12. 已知点关于轴对称的点在第一象限,则的取值范围是 .13. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.
 14. 如图,已知直线和直线交于点 , 若二元一次方程组的解为、 , 则关于.
14. 如图,已知直线和直线交于点 , 若二元一次方程组的解为、 , 则关于. 15. 喜欢探索数学知识的小明遇到一个新的定义:对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个正整数为“和谐组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如1,4,9这三个数, , , , 其结果都是整数,所以1,4.9三个数称为“和谐组合”,其中最小算术平方根是2,最大算术平方根是6.若2,8,18三个数是“和谐组合”,则其中最小算术平方根与最大算术平方根的和是 .
15. 喜欢探索数学知识的小明遇到一个新的定义:对于三个正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个正整数为“和谐组合”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如1,4,9这三个数, , , , 其结果都是整数,所以1,4.9三个数称为“和谐组合”,其中最小算术平方根是2,最大算术平方根是6.若2,8,18三个数是“和谐组合”,则其中最小算术平方根与最大算术平方根的和是 .三、解答题(共7题,共55分)
-
16. 一个正数x的两个平方根分别是2a﹣1与﹣a+2,求a的值和这个正数x的值.17.(1)、解二元一次方程组 .(2)、已知(1)中的解满足0<ax+3y<6.求正整数a的算术平方根.18. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
 19. 甲、乙两名队员参加射击训练,将10次成绩分别制成如图所示的两个统计图:
19. 甲、乙两名队员参加射击训练,将10次成绩分别制成如图所示的两个统计图: (1)、根据以上信息,整理分析数据如表:
(1)、根据以上信息,整理分析数据如表:平均成绩(环)
众数(环)
中位数
方差
甲
7
a
7
c
乙
7
8
b
4.2
填空:a= , b= , c=;
(2)、根据以上数据分析,请你运用所学统计知识,任选两个角度评价甲、乙两名队员哪位队员的射击成绩更好.20. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.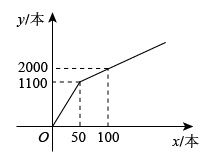 (1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.
(1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?
21. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共个,某电商内部信息表给出其进价与售价间的关系如表:篮球
足球
进价元个
售价元个
(1)、学校用元以进价购进这批篮球和足球,求购进篮球和足球各多少个;
(2)、设该电商所获利润为单位:元 , 购进篮球的个数为单位:个 , 请写出与之间的函数表达式不要求写出的取值范围;
(3)、因资金紧张,学校的进货成本只能在元的限额内,请为学校设计一种进货方案使得尽可能多地购买篮球和足球,同时要使电商利润最小;并求出利润的最小值.22. 阅读材料:如图1,已知Rt△ABC中,∠C=90°,请用尺规作图在AB边上求作点P,使得∠BPC+∠ACP=90°.小明提出想法:如图2,假设点P为所求作的点,连接CP,此时有∠BPC+∠ACP=90°,因为∠BCP+∠ACP=90°,所以∠BPC=∠BCP,从而得到:BP=BC.
由此想法得到如下作图方法:如图2,以点B为圆心,BC为半径画弧,该弧与AB相交于点P,则点P即为所作的点.
根据以上材料,完成下面两个问题:
 (1)、请你类比上述作图方法,在图2中,用尺规作图在AB边上求作点Q,使得∠CQB+∠A=180°.(2)、在(1)的条件下,
(1)、请你类比上述作图方法,在图2中,用尺规作图在AB边上求作点Q,使得∠CQB+∠A=180°.(2)、在(1)的条件下,①若AC=6,AB=10,求PQ的长.
②请直接写出∠PCQ与∠B之间的数量关系是 .