浙教版数学七年级上册期末冲刺满分攻略1 实数的认识及其分类

试卷更新日期：2023-12-11 类型：复习试卷

进入出卷网下载

一、选择题

1. 对于实数 $x$ ，我们规定[x]表示不大于 $x$ 的最大整数，如 $[2] = 2 ， [1.5] = 1 ，$ $[- 2.3] = - 3$ .对数99进行如下操作： $99 \overset{第 1 次}{\to} [\sqrt{99}]$ $= 9 \overset{第 2 次}{\to} [\sqrt{9}]$ $= 3 \overset{第 3 次}{\to} [\sqrt{3}]$ =1，这样对数99只需进行3次操作后变成1，类似地，使数520变为1需要进行操作的次数是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 有下列各数： $\frac{π}{3} ， \sqrt[3]{9} ， - \sqrt{4} ，$ $0.34 ， \frac{5}{7} ，$ $2.1717717771$ …(自左向右每两个“1”之间依次多一个“7”）.其中无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列说法正确的是（）
①无理数是无限不循环小数；②所有无理数都能用数轴上的点表示；
③绝对值等于其本身的数是0；④两个无理数的和可能为有理数.

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
4. 在生产图纸上通常用 $\emptyset 30 0_{- 0.5}^{+ 0.2}$ 来表示轴的加工要求，这里 $\emptyset 300$ 表示直径是 $300 m m$ ， $+ 0.2$ 和 $- 0.5$ 是指直径在 $(300 - 0.5) m m$ 到 $(300 + 0.2) m m$ 之间的产品都属于合格产品.现加工一批轴，尺寸要求是 $\emptyset 4 5_{- 0.3}^{+ 0.2}$ ，则下面产品合格的是（）

A、 $44.6 m m$ B、 $44.8 m m$ C、 $45.3 m m$ D、 $45.5 m m$

查看试题解析
5. 估计 $\sqrt{7} + 2$ 的范围是（）

A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间

查看试题解析
6. 若正数 $x$ 满足 $x^{2} = 18$ ，则下列整数中与 $x$ 最接近的是（）

A、2 B、3 C、4 D、5

查看试题解析
7. 若整数a满足 $\sqrt{7}$ <a< $\sqrt{15}$ ，则整数a是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图所示，面积为5的正方形 $A B C D$ 的顶点 $A$ 在数轴上，且点 $A$ 表示的数为1，若点 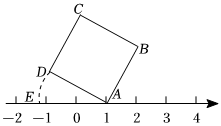$E$ 在数轴上 $($ 点 $E$ 在点 $A$ 左侧 $)$ ，且 $A D = A E$ ，则点 $E$ 所表示的数为（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $- \sqrt{5} - 1$ D、 $- \sqrt{5} + 1$

查看试题解析
9. 根据以下程序，当输入 $x = \sqrt{7}$ 时，输出的结果是（）

A、0 B、1 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
10. 下列说法正确的是（）

A、 $\frac{\sqrt{2}}{2}$ 是分数 B、16的平方根是±4，即 $\sqrt{16} = \pm 4$ C、8.30万精确到百分位 D、若 $\sqrt{a - 2022} + | b + 1 | = 0$ ，则 $b^{a} = 1$

查看试题解析

二、填空题

11. 如果涨潮时水位升高 $7.2 m$ ，水位变化记作 $+ 7.2 m$ ，那么退潮时水位下降 $2.3 m$ ，水位变化可记作 $m$ .

查看试题解析
12. 若a与b互为相反数，m与n互为倒数，k的算术平方根为 $\sqrt{2}$ ，则 $2022 a + 2021 b + m n b + k^{2}$ 的值为．

查看试题解析
13. 实数 $\sqrt{7}$ 的整数部分为a，小数部分为b，则 $\sqrt{7}$ （a²+ab）= ．

查看试题解析
14. 点A，B在数轴上，以AB为边作正方形，该正方形的面积是7．若点A对应的数是－2，则点B对应的数是．

查看试题解析
15. 长方形 $ABCD$ 的边 $AD$ 长为3， $AB$ 长为1，点 $A$ 在数轴上对应的数是1，以点 $A$ 为圆心，对角线 $AC$ 长为半径画弧，交数轴于点 $E$ ，则这个点 $E$ 表示的实数是.

查看试题解析
16. 对于实数 $a 、 b$ ，定义 $m i n {a ， b}$ 的含义为∶ 当 $a < b$ 时， $m i n {a ， b} = a$ ；当 $a > b$ 时， $m i n {a ， b} = b$ ，例如∶ $m i n {1 ， - 2} = - 2$ .已知 $m i n {\sqrt{30} ， a} = a ， m i n {\sqrt{30} ， b} = \sqrt{30}$ ，且 $a$ 和 $b$ 为两个连续正整数，则 $2 a - b$ 的值为.

查看试题解析

三、解答题

17. 把下面的数填入它所属于的集合的大括号内（填序号）
①-5.3，②+5，③20%，④0，⑤ $- \frac{7}{2}$ ， ⑥-7，⑦-∣-3∣，⑧-(-1.8)
正数集合｛        ｝
整数集合｛        ｝
分数集合｛        ｝
有理数集合｛        ｝

查看试题解析
18. 已知下列各数： $- 4 ， - 1$ 的相反数， $- π ， | - 3 | ， \sqrt{2}$ .

(1)、将上述各数表示在数轴上.

(2)、将上述各数按从小到大的顺序用“＜”连接.

查看试题解析
19. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $b - 9$ 的立方根是 $2$ ， $c$ 是 $\sqrt{12}$ 的整数部分．

(1)、求 $a$ 、 $b$ 、 $c$ 的值；

(2)、若 $x$ 是 $\sqrt{12}$ 的小数部分，求 $x - \sqrt{12} + 12$ 的值．

查看试题解析
20. 已知七个实数 $- \sqrt{5}$ ， $\frac{3}{2}$ ， 4，5.3， $- \sqrt[3]{64}$ ， 0， $π$ ，其中三个数已在数轴上分别用点A、B、C表示.

(1)、点A表示数，点B表示数，点C表示数.

(2)、在数轴上精确地表示出剩下的4个数（提示：注意观察正方形 $A P Q R$ 的面积），并将轴上精确地表示所有的数用“＜”连接.
∴ < < < < < < < .

(3)、将上列各数分别填入相应括号的横线上：
整数：{ }

分数：{ }

无理数：{ }.

查看试题解析
21. 中国古代的数理天文学通常都是以分数的形式选择历法中用到的天文学常数.由于这些天文学常数基本上都是无理数，因此，历法家们设计了一些算法用来挑选合适的有理数去逼近这些常数，这样的方法在数学上被称作“实数的有理逼近”.我国南北朝时期数学家何承天发明的“调日法”便是利用分数的加成性质而设计的一种实数的有理逼近算法，其步骤大体如下：设实数x的不足近似值和过剩近似值分别为 $\frac{b}{a}$ 和 $\frac{d}{c}$ （即有 $\frac{b}{a}$ ＜x＜ $\frac{d}{c}$ ，其中a，b，c，d为正整数），则 $\frac{b + d}{a + c}$ 是x的更为精确的近似值.例如：已知 $\frac{157}{50} ＜ π ＜ \frac{22}{7}$ ，则利用一次“调日法”后可得到π的一个更为精确的近似分数为 $\frac{157 + 22}{50 + 7} = \frac{179}{57}$ ；由于 $\frac{179}{57}$ ≈3.1404＜π，再由 $\frac{179}{57}$ $＜ π ＜ \frac{22}{7}$ ，可以再次使用“调日法”得到π的更为精确的近似分数 $\frac{201}{64}$ .

(1)、现已知 $\frac{11}{5} ＜ \sqrt{5} ＜ \frac{12}{5}$ ，
使用一次“调日法”计算 $\sqrt{5}$ 的一个更为精确的近似分数为；
使用二次“调日法”计算 $\sqrt{5}$ 的一个更为精确的近似分数为；
使用三次“调日法”计算 $\sqrt{5}$ 的一个更为精确的近似分数为；

(2)、 $\sqrt{5}$ 的整数部分为x，小数部分为y，求x+2y的值.

查看试题解析