2023-2024学年浙教版数学七年级(上)期末仿真模拟卷(一)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列说法不正确的是( )A、0既不是正数,也不是负数 B、1是绝对值最小的有理数 C、一个有理数不是整数就是分数 D、0的绝对值是02. 四个有理数 , 其中最小的是( )A、-2 B、-1 C、0 D、23. 太阳的中心温度是1 550万℃,1 550万用科学记数法可表示为( )A、1.55×106 B、15.5×106 C、1.55×107 D、0.155×1084. 按照如图所示的操作步骤进行计算,若输人的值为-3,则输出的值为( )
 A、0 B、4 C、55 D、605. 下列各组数中,互为相反数的是( )A、与 B、与 C、与 D、与6. 小兰房间窗户的装饰物如下图所示,该装饰物由两个半圆组成(半径相同),则窗户中能射进阳光的部分的面积为( )
A、0 B、4 C、55 D、605. 下列各组数中,互为相反数的是( )A、与 B、与 C、与 D、与6. 小兰房间窗户的装饰物如下图所示,该装饰物由两个半圆组成(半径相同),则窗户中能射进阳光的部分的面积为( ) A、ab-b2 B、ab- b2 C、ab- b2 D、ab- b27. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )
A、ab-b2 B、ab- b2 C、ab- b2 D、ab- b27. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )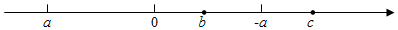 A、 B、 C、 D、08. 根据等式的性质,下列变形不成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 有一批货物共x吨,由一个车队进行装运,若每辆车装9吨,恰好装完;若每辆车装8吨,还有16吨没运完,则下列所列方程中,正确的是( )A、 B、 C、 D、10. 如图,C,D在线段上,下列四个说法:
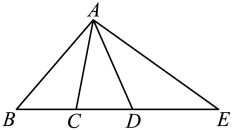
A、 B、 C、 D、08. 根据等式的性质,下列变形不成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 有一批货物共x吨,由一个车队进行装运,若每辆车装9吨,恰好装完;若每辆车装8吨,还有16吨没运完,则下列所列方程中,正确的是( )A、 B、 C、 D、10. 如图,C,D在线段上,下列四个说法:①直线上以B,C,D,E为端点的线段共有6条;
②图中有3对互为补角的角;
③若 , , 则以A为顶点的所有小于平角的角的度数和为370°;
④若 , , , 点F是线段上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为25
其中正确说法的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共24分)
-
11. 比较大小: (填 或者 或者 ).12. 甲、乙两地的海拔高度分别为20m和 , 则甲地比乙地高13. 计算:= .
14. 若和是同类项,则m的值是 .15. 若∠α=42°24',∠β=15.3°,则∠α与∠β的和等于16. 学校为“中国共产党建党100周年合唱比赛”印制宣传册,某复印店的收费标准如下:①印制册数不超过100册时,每册2元;
②印制册数超过100册但不超过300册时,每册按原价打八折;
③印制册数超过300册时,前300册每册按原价打八折,超过300册的部分每册按原价打六折;
学校在复印店印制了两次宣传册,分别花费192元和576元,如果学校把两次复印的宣传册合并为一次复印,则可节省元.
三、解答题(共8题,共66分)
-
17. 已知数轴上,点A对应的数为a,点B对应的数为b,且 .(1)、若 ,求a的值.(2)、若点A和点B分别位于原点O的两侧, ,求a与b的值.18. 计算:.
毛毛在做作业时,发现题中有一个数字被墨水污染了.如果计算结果等于14,求被污染的数字.
19. 已知正数x的平方根是a和(1)、当时,求a的值.(2)、若 , 求x的值.20. 已知 A=3x2+3y2-2xy,B=xy-2y2-2x2.求:
(1)、2A-3B.(2)、若|2x-3|=1,y2=9,|x-y|=y-x,求 2A-3B 的值.(3)、若 x=2,y=-4 时,代数式 ax3+by+5=17,那么当 x=-4,y=-时,求代数式3ax-24by3+6 的值.21. 如图是2022年11月的日历,用一个方框在日历中任意框出4个代表日期的数

 (1)、;(2)、设.
(1)、;(2)、设.①若 , 求a的值;
②S的值能否为36?请说明理由.
22. 如图,已知直线 , 射线 , 线段. (1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.
(1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.
