【北师大版】2023-2024学年数学九年级（上）期末仿真模拟试题（一）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，在矩形ABCD中，对角线AC，BD交于点O，若AC=14，则OB的长为（）

A、7 B、6 C、5 D、2

查看试题解析
2. 下列命题正确的是（）

A、三视图是中心投影 B、小华观察牡丹花，牡丹花就是视点 C、球的三视图均是半径相等的圆 D、阳光从矩形窗子里照射到地面上，得到的光区仍是矩形

查看试题解析
3. 如图，在 $▱ A B C D$ 中，对角线AC与BD相交于点O，如果添加一个条件，可推出 $▱ A B C D$ 是菱形，那么这个条件可以是（）

A、 $A B = A C$ B、 $A C = B D$ C、 $A C ⊥ B D$ D、 $A B ⊥ A C$

查看试题解析
4. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，配方结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
5. 若方程 $x^{2} - 3 x + m = 0$ 有两个不相等的实数根，则m的值可以是（）

A、5 B、4 C、3 D、2

查看试题解析
6. 我国快递业务逐年增加，2019年至2021年我国快递业务收入由7500亿元增加到9000亿元.设我国2019年至2021年快递业务收入的年平均增长率为x ，则可列方程为（　　）

A、 $7500 (1 + 2 x) = 9000$ B、 $7500 \times 2 (1 + x) = 9000$ C、 $7500 {(1 + x)}^{2} = 9000$ D、 $7500 + 7500 (1 + x) + 7500 {(1 + x)}^{2} = 9000$

查看试题解析
7. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（）

A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现2点朝上 C、从一个装有3个红球2个黑球的袋子中任取一球，取到的是黑球 D、从一个装有3个红球2个黑球的袋子中任取两球，取到的是黑球

查看试题解析
8. 常言道：失之毫厘，谬以千里．当人们向太空发射火箭或者描述星际位置时，需要非常准确的数据． $1^{″}$ 的角真的很小．把整个圆等分成360份，每份这样的弧所对的圆心角的度数是 $1 °$ ． $1 ° = 6 0^{'} = 360 0^{″}$ ．若一个等腰三角形的腰长为1千米，底边长为4.848毫米，则其顶角的度数就是 $1^{″}$ ．太阳到地球的平均距离大约为 $1.5 \times 1 0^{8}$ 千米．若以太阳到地球的平均距离为腰长，则顶角为 $1^{″}$ 的等腰三角形底边长为（　　）

A、24.24千米 B、72.72千米 C、242.4千米 D、727.2千米

查看试题解析
9. 在平面直角坐标系中，已知反比例函数 $y = \frac{k}{x}$ 的图象经过 $A (x_{1} ， y_{1}) ， B (2 ， y_{2}) ， C (3 ， 2)$ ，则下列说法不正确的是（）

A、 $k = 6$ B、函数图象位于第一、三象限 C、已知点 $D (2 ， 0)$ ，连接OB，BD，则 $S_{△ O B D} = 3$ D、若 $x_{1} < 2$ ，则 $y_{1} > y_{2}$

查看试题解析
10. 如图，在正方形 $A B C D$ 中， $A B = 4$ ， $E$ 为对角线 $A C$ 上与点 $A$ ， $C$ 不重合的一个动点，过点 $E$ 作 $E F ⊥ A B$ 于点 $F$ ， $E G ⊥ B C$ 于点 $G$ ，连接 $D E$ ， $F G$ .给出下列结论：① $D E = F G$ ；② $D E ⊥ F G$ ；③ $∠ B F G = ∠ A D E$ ；④ $F G$ 的最小值为3.其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共15分）

11. 如图是某几何体的三视图，其俯视图为等边三角形，则该几何体的左视图的面积为 $c m^{2}$

查看试题解析
12. 已知 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两根，则 $\frac{2}{x_{1}} + \frac{2}{x_{2}} =$ .

查看试题解析
13. 一个不透明的口袋中有4个完全相同的小球，球上分别标有数字-2，0，1，4.随机摸出一个小球记作m，然后放回，再随机摸出一个小球记作n，则方程 $m x^{2} - 2 x + n ＝ 0$ 是关于x的一元二次方程且此方程无解的概率为 .

查看试题解析
14. 如图，小明与大树之间放置了一面平面镜，平面镜到小明的距离是2米、到大树的距离是6米时，小明恰好能从平面镜中看见大树的树尖，若小明的眼睛距离地面1.5米，则大树的高为米.

查看试题解析
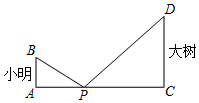15. 如图，在一块边长为 $2 \sqrt{2}$ 的正方形纸板ABCD，做成如图1所示的一套七巧板（点O为正方形纸板对角线的交点），点E、F分别为AD、CD的中点.若将图1中的七巧板拼出如图2所示的“鱼形”，则“鱼尾”MN的长为.

查看试题解析

三、解答题（共7题，共55分）

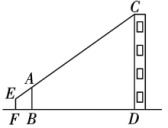
16. 解方程．

(1)、2x²+3x-1＝0；

(2)、3x+6＝（x+2）² ．

查看试题解析
17. 学习了相似三角形相关知识后，小明和同学们想利用“标杆”测量大楼的高度.如图，小明站立在地面点F处，他的同学在点B处竖立“标杆”AB，使得小明的头顶E、标杆顶端A、大楼顶端C在一条直线上（点F、B、D也在一条直线上）.已知小明的身高EF=1.5米，“标杆”AB=2.5米，BD=23米，FB=2米，EF、AB、CD均垂直于地面BD.求大楼的高度CD.

查看试题解析
18. 如图，一个零件形如一个圆柱体削去底面圆的四分之一部分的柱体，底面圆的半径为 $2 cm$ ．

(1)、请画出该零件的三视图；

(2)、若用该零件的俯视图围成一个圆锥，求这个圆锥的高．

查看试题解析
19. 某厂有一批可降解的外卖餐盒准备出售，现从中随机抽取一部分外卖餐盒，根据这些餐盒的价格（单位：元）分别绘制了如图1，图2所示的扇形统计图和条形统计图，相同价格的餐盒除颜色外均相同。请根据相关信息，解答下列问题．

(1)、随机抽取的外卖餐盒的数量为个；图中a的值为；b的值为；

(2)、在这组数据中，价格为2元的外卖餐盒颜色如下：2个白色，1个红色，1个黄色，现从这4个餐盒中随机抽取2个外卖餐盒，请利用画树状图的方法求抽到一个白色餐盒和一个红色餐盒的概率．

查看试题解析
20. 如图，直线 $y = \frac{3}{2} x$ 与双曲线 $y = \frac{k}{x} (k \neq 0)$ 交于A ， $B$ 两点，点A的坐标为 $(m ， - 3)$ ，点 $C$ 是双曲线第一象限分支上的一点，连结 $B C$ 并延长交 $x$ 轴于点 $D$ ，且 $B C = 2 C D$ ．

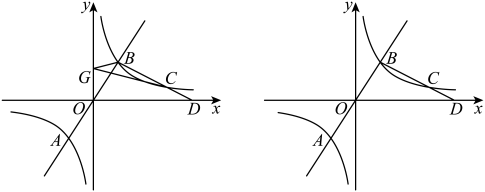(1)、求 $k$ 的值，并直接写出点 $B$ 的坐标；

(2)、点 $G$ 是 $y$ 轴上的动点，连结 $G B$ ， $G C$ ，求 $G B + G C$ 的最小值和点 $G$ 坐标；

(3)、 $P$ 是坐标轴上的点， $Q$ 是平面内一点，是否存在点 $P$ ， $Q$ ，使得四边形 $A B P Q$ 是矩形？若存在，请求出所有符合条件的点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析
21. 小彬做了探究物体投影规律的实验，并提出了一些数学问题请你解答：

(1)、如图1，白天在阳光下，小彬将木杆 $A B$ 水平放置，此时木杆在水平地面上的影子为线段 $A^{'} B^{'}$ .
①若木杆 $A B$ 的长为 $1 m$ ，则其影子 $A^{'} B^{'}$ 的长为 $m$ ；

②在同一时刻同一地点，将另一根木杆 $C D$ 直立于地面，请画出表示此时木杆 $C D$ 在地面上影子的线段 $D M$ ；

(2)、如图2，夜晚在路灯下，小彬将木杆 $E F$ 水平放置，此时木杆在水平地面上的影子为线段 $E^{'} F^{'}$ .
①请在图中画出表示路灯灯泡位置的点 $P$ ；

②若木杆 $E F$ 的长为 $1 m$ ，经测量木杆 $E F$ 距离地面 $1 m$ ，其影子 $E^{'} F^{'}$ 的长为 $1.5 m$ ，则路灯 $P$ 距离地面的高度为 $m$ .

查看试题解析
22. 综合与实践
问题情境：在综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动，请你解答各小组活动中产生的问题 $.$ 如图所示，在矩形 $A B C D$ 中， $A B = 4 c m$ ， $A D = 8 c m$ ，将矩形纸片进行折叠：

(1)、问题解决：如图 $1$ ，奋斗小组将该矩形沿对角线 $A C$ 折叠，点 $B$ 的对应点为点 $B'$ ，则 $D E =$ $c m$ ， $S_{△ A E C} =$ $c m^{2}$ ；

(2)、实践探究：如图 $2$ ，希望小组将矩形 $A B C D$ 沿着 $E F （$ 点 $E$ ， $F$ 分别在边 $A D$ ，边 $B C$ 上 $）$ 所在的直线折叠，点 $B$ 的对应点为点 $D$ ，连接 $B E$ ，
$①$ 试判断四边形 $B E D F$ 的形状，并说明理由；
$②$ 求折痕 $E F$ 的长．

查看试题解析