2023-2024学年广东省(人教版)九年级(上)数学期末模拟卷(三)
试卷更新日期:2023-12-11 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 将一元二次方程化成的形式,则( )A、-1 B、-2023 C、1 D、20232. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚(如图),那么点B从开始至结束所经过的路径长为( ).
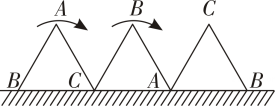 A、 B、 C、4 D、2+3. 已知关于x的一元二次方程x2-mx+n=0,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( )
A、 B、 C、4 D、2+3. 已知关于x的一元二次方程x2-mx+n=0,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( )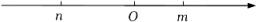 A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定4. 已知抛物线的对称轴为直线 , 若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是( )A、 B、 C、 D、5. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段OP的长为( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定4. 已知抛物线的对称轴为直线 , 若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是( )A、 B、 C、 D、5. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段OP的长为( )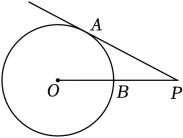 A、3 B、 C、6 D、96. 若a、b是关于x的一元二次方程x2-6x+n+1=0的两根,且等腰三角形三边长分别为a、b、4,则n的值为( )A、8 B、7 C、8或7 D、9或87. 已知正六边形的边长为4,则这个正六边形外接圆的半径为( )A、2 B、2 C、4 D、48. 一枚飞任意投掷到如图所示的同心圆镖盘上,此镖盘上有两个同心圆,三条直径把大圆分成六等份,飞镖落在白色区域的概率为( )
A、3 B、 C、6 D、96. 若a、b是关于x的一元二次方程x2-6x+n+1=0的两根,且等腰三角形三边长分别为a、b、4,则n的值为( )A、8 B、7 C、8或7 D、9或87. 已知正六边形的边长为4,则这个正六边形外接圆的半径为( )A、2 B、2 C、4 D、48. 一枚飞任意投掷到如图所示的同心圆镖盘上,此镖盘上有两个同心圆,三条直径把大圆分成六等份,飞镖落在白色区域的概率为( )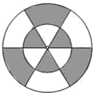 A、 B、 C、 D、9. 如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )
A、 B、 C、 D、9. 如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开。已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长。小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2。则:( )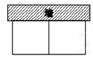 A、小明正确,小亮错误 B、小明错误,小亮正确 C、两人均正确 D、两人均错误10. 如图,抛物线的对称轴为直线 , 经过点 . 下列结论:①;②;③;④抛物线经过点和 , 则;⑤(为任意实数).其中,正确结论的个数是( )
A、小明正确,小亮错误 B、小明错误,小亮正确 C、两人均正确 D、两人均错误10. 如图,抛物线的对称轴为直线 , 经过点 . 下列结论:①;②;③;④抛物线经过点和 , 则;⑤(为任意实数).其中,正确结论的个数是( )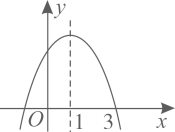 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 函数y=x2﹣5的最小值是 .12. 抛物线y=2(x﹣3)2+7的顶点坐标为 .13. 若一元二次方程的两根分别为m与n,则 .14. 如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转60°,点B、C的对应点分别为D、E,点D在 上,则阴影部分的面积为 .
 15. 如图,在中, , 点是的内心,则度.
15. 如图,在中, , 点是的内心,则度.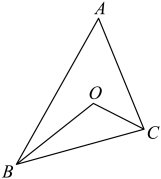
三、解答题
-
16. 解答题(1)、解方程: ;(2)、用配方法解方程: .17. 如图,在△ABC中,∠A=∠B=30°.
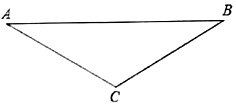 (1)、尺规作图:在线段AB上找一点O,以O为圆心作圆,使⊙O经过B,C两点.(2)、求证:AC与(1)中所做的⊙O相切.18. 如图,是以为斜边的等腰直角三角形,其内部的4段弧均等于以BC为直径的圆周,求图中阴影部分的面积.
(1)、尺规作图:在线段AB上找一点O,以O为圆心作圆,使⊙O经过B,C两点.(2)、求证:AC与(1)中所做的⊙O相切.18. 如图,是以为斜边的等腰直角三角形,其内部的4段弧均等于以BC为直径的圆周,求图中阴影部分的面积.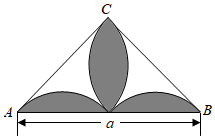 19. 现有A、B两个不透明的袋子,A袋中的两个小球分别标记数字1,2;B袋中的三个小球分别标记数字3,4,5.这五个小球除标记的数字外,其余完全相同.分别将A、B两个袋子中的小球摇匀,然后小明从A、B袋中各随机摸出一个小球,请利用画树状图或列表的方法,求小明摸出的这两个小球标记的数字之和为5的概率.20. 某市为鼓励居民节约用水,对居民用水实行阶梯收费,每户居民用水量每月不超过a吨时,每吨按0.3a元缴纳水费;每月超过a吨时,超过部分每吨按0.4a元缴纳水费.(1)、若a=12,某户居民3月份用水量为22吨,则该用户应缴纳水费多少元?(2)、若如表是某户居民4月份和5月份的用水量和缴费情况:
19. 现有A、B两个不透明的袋子,A袋中的两个小球分别标记数字1,2;B袋中的三个小球分别标记数字3,4,5.这五个小球除标记的数字外,其余完全相同.分别将A、B两个袋子中的小球摇匀,然后小明从A、B袋中各随机摸出一个小球,请利用画树状图或列表的方法,求小明摸出的这两个小球标记的数字之和为5的概率.20. 某市为鼓励居民节约用水,对居民用水实行阶梯收费,每户居民用水量每月不超过a吨时,每吨按0.3a元缴纳水费;每月超过a吨时,超过部分每吨按0.4a元缴纳水费.(1)、若a=12,某户居民3月份用水量为22吨,则该用户应缴纳水费多少元?(2)、若如表是某户居民4月份和5月份的用水量和缴费情况:月份
用水量(吨)
交水费总金额(元)
4
18
62
5
24
86
根据上表数据,求规定用水量a的值
21. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.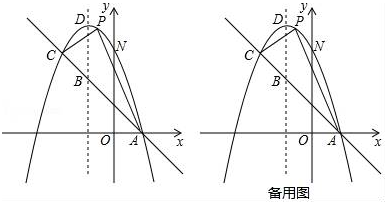 (1)、求抛物线及直线AC的函数关系式;(2)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;(3)、在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.22. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)、求抛物线及直线AC的函数关系式;(2)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;(3)、在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.22. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).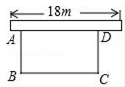 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.甲
乙
丙
单价(元/棵)
14
16
28
合理用地(m2/棵)
0.4
1
0.4
23. 如图1,为的外接圆,半径为6, , , 点为优弧上异于的一动点,连接 .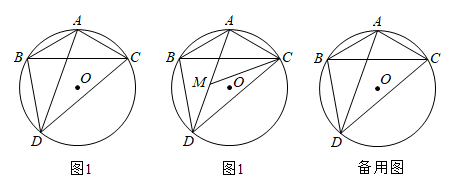 (1)、求证:平分;(2)、如图2,平分 , 且与交于 .
(1)、求证:平分;(2)、如图2,平分 , 且与交于 .花花同学认为:无论点运动到哪里,始终有;
都都同学认为:的长会随着点运动而变化.
你赞同谁的观点,请说明理由;
(3)、求的最大值.