2023-2024学年浙教版数学八年级(上)期末仿真模拟卷(杭州适用3)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列命题中,是真命题的是( )A、如果两条直线垂直于同一条直线,那么这两条直线平行 B、过一点有且只有一条直线与已知直线平行 C、同一平面内,过一点有且只有一条直线垂直于已知直线 D、同位角相等3. 如图,△ABC与△A1B1C1关于直线l对称,若∠B =25°,∠A=35°,则∠C的度数为( )
2. 下列命题中,是真命题的是( )A、如果两条直线垂直于同一条直线,那么这两条直线平行 B、过一点有且只有一条直线与已知直线平行 C、同一平面内,过一点有且只有一条直线垂直于已知直线 D、同位角相等3. 如图,△ABC与△A1B1C1关于直线l对称,若∠B =25°,∠A=35°,则∠C的度数为( ) A、90° B、110° C、120° D、125°4. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( )
A、90° B、110° C、120° D、125°4. 如图,在中, , 的垂直平分线交于点D,交于点E,若 , 则( ) A、 B、 C、 D、5. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50<x<80 B、50≤x≤80 C、50≤x<80 D、50<x≤806. 已知关于的不等式组的所有整数解的和为-5,则的取值范围为( )A、或 B、或 C、 D、7. 若点在第四象限,则点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 点M(-5,2)关于y轴对称的点的坐标为( )A、(-5,-2) B、(5,-2) C、(5,2) D、(-5,2)9. 已知火车的速度是120千米/时,则火车行驶的路程s(千米)与时间t(时)之间的关系是s=120t.在此变化过程中,变量是( )A、速度、路程 B、速度、时间 C、路程、时间 D、速度、路程与时间10. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( )
A、 B、 C、 D、5. 小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )A、50<x<80 B、50≤x≤80 C、50≤x<80 D、50<x≤806. 已知关于的不等式组的所有整数解的和为-5,则的取值范围为( )A、或 B、或 C、 D、7. 若点在第四象限,则点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 点M(-5,2)关于y轴对称的点的坐标为( )A、(-5,-2) B、(5,-2) C、(5,2) D、(-5,2)9. 已知火车的速度是120千米/时,则火车行驶的路程s(千米)与时间t(时)之间的关系是s=120t.在此变化过程中,变量是( )A、速度、路程 B、速度、时间 C、路程、时间 D、速度、路程与时间10. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 如图,△ABC中,BC的垂直平分线l与AC相交于点D,若△ABD的周长为12cm,
则AB+AC=cm.
 12. 已知直角三角形的一条直角边长与斜边长分别为6 cm和10 cm,则这个直角三角形斜边上的中线长为cm,斜边上的高线长为cm.13. 知P1(a-1,4)和P2(2,b)关于x轴对称,则(a+b)2021的值为 .14. 函数y=的自变量x的取值范围为 .15. 若关于的一元一次不等式组无解,则的取值范围是16. 如图,中,、的角平分线、交于点 , 延长、 , 于 , 于 , 则下列结论:①平分;②;③;④ . 其中正确结论序号是 .
12. 已知直角三角形的一条直角边长与斜边长分别为6 cm和10 cm,则这个直角三角形斜边上的中线长为cm,斜边上的高线长为cm.13. 知P1(a-1,4)和P2(2,b)关于x轴对称,则(a+b)2021的值为 .14. 函数y=的自变量x的取值范围为 .15. 若关于的一元一次不等式组无解,则的取值范围是16. 如图,中,、的角平分线、交于点 , 延长、 , 于 , 于 , 则下列结论:①平分;②;③;④ . 其中正确结论序号是 .
三、解答题(共7题,共66分)
-
17.(1)、解不等式 , 并把它的解集表示在数轴上.(2)、解不等式组 .18. 如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,且点A,C,E在同一条直线上.

求证:
(1)、△DAB≌△ECB;(2)、作BF⊥AE于F,若AD=3,AF=1,求BE的长.19. 如图,在直角坐标系中,将线段平移至 , 已知 , 连接 , 点D在射线上移动(不与点O、A重合).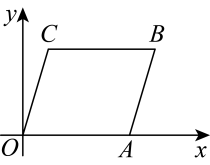 (1)、直接写出点C的坐标;(2)、点D在运动过程中,是否存在的面积等于320. 如图,A,B是分别在x轴上的原点左右侧的点,点P(2,m)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOC=10.
(1)、直接写出点C的坐标;(2)、点D在运动过程中,是否存在的面积等于320. 如图,A,B是分别在x轴上的原点左右侧的点,点P(2,m)在第一象限内,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOC=10. (1)、求点A的坐标及m的值;(2)、若S△BOP=S△DOP , 求直线BD的解析式;(3)、在(2)的条件下,直线AP上是否存在一点Q,使△QAO的面积等于△BOD面积?若存在,求出点Q的坐标;若不存在,请说明理由.21. 如图
(1)、求点A的坐标及m的值;(2)、若S△BOP=S△DOP , 求直线BD的解析式;(3)、在(2)的条件下,直线AP上是否存在一点Q,使△QAO的面积等于△BOD面积?若存在,求出点Q的坐标;若不存在,请说明理由.21. 如图 (1)、如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的AM、 AN上,且AB=AC, CF⊥AE于点F, BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图2,点B、C分别在∠MAN的边AM AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、OCAF的外角,已知AB=AC, 且∠1=∠2=∠BAC.
(1)、如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的AM、 AN上,且AB=AC, CF⊥AE于点F, BD⊥AE于点D.求证:△ABD≌△CAF;(2)、如图2,点B、C分别在∠MAN的边AM AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、OCAF的外角,已知AB=AC, 且∠1=∠2=∠BAC.求证:△ABE≌ △CAF;
(3)、如图3,在△ABC中,AB=AC,AB>BC. 点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为27,直接写出△ACF与△BDE的面积之和.22. 规定:在平面直角坐标系内,某直线绕原点顺时针旋转 , 得到的直线称为的“旋转垂线”. (1)、求出直线的“旋转垂线”的解析式;(2)、若直线的“旋转垂线”为直线求证:;(3)、如图,在平面直角坐标系中,点 , 点 , 点是直线上一点,度,求点的坐标.23. 如图 , 在平面直角坐标系中,直线分别与轴,轴交于点 , , 过点作轴的垂线,与直线交于点 .
(1)、求出直线的“旋转垂线”的解析式;(2)、若直线的“旋转垂线”为直线求证:;(3)、如图,在平面直角坐标系中,点 , 点 , 点是直线上一点,度,求点的坐标.23. 如图 , 在平面直角坐标系中,直线分别与轴,轴交于点 , , 过点作轴的垂线,与直线交于点 .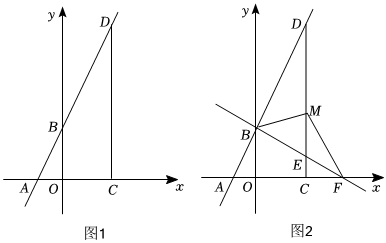 (1)、求点的坐标;(2)、点是线段上一动点,直线与轴交于点 .
(1)、求点的坐标;(2)、点是线段上一动点,直线与轴交于点 .若的面积为 , 求点的坐标;
如图 , 当点在轴正半轴上时,将直线绕点逆时针旋转后的直线与线段交于点 , 连接 , 若 , 求线段的长.