2023-2024学年高中数学人教A版必修二 8.3 简单几何体的表面积和体积同步练习

试卷更新日期：2023-12-11 类型：同步测试

进入出卷网下载

一、选择题

1. 正四棱台上、下底面边长分别为 $2 c m ， 4 c m$ ，侧棱长 $2 c m$ ，则棱台的侧面积为（）

A、 $12 \sqrt{3} c m^{2}$ B、 $3 \sqrt{3} c m^{2}$ C、 $24 c m^{2}$ D、 $6 c m^{2}$

查看试题解析
2. 庑殿式屋顶是中国古代建筑中等级最高的屋顶形式，分为单檐庑殿顶与重檐庑殿顶．单檐庑殿顶主要有一条正脊和四条垂脊，前后左右都有斜坡（如图①）（如图②），若四边形ABCD是矩形，AB∥EF，且AB=CD=2EF=2BC=4，EA＝ED＝FB＝FC＝3，则五面体FE﹣ABCD的表面积为（）

A、48 B、 $32 \sqrt{5}$ C、 $16 + 16 \sqrt{5}$ D、 $32 + 16 \sqrt{5}$

查看试题解析
3. 如图，圆锥 $P O$ 的底面直径和高均是4，过 $P O$ 的中点 $O_{1}$ 作平行于底面的截面，以该截面为底面挖去一个圆柱，则剩下几何体的表面积为（）

A、 $(7 + 4 \sqrt{5}) π$ B、 $(8 + 4 \sqrt{5}) π$ C、 $(9 + 4 \sqrt{5}) π$ D、 $(6 + 4 \sqrt{5}) π$

查看试题解析
4. 已知某圆锥的侧面展开图是一个半径为r的半圆，且该圆锥的体积为 $3 π$ ，则r=（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $2 \sqrt{3}$ D、3

查看试题解析
5. 阿基米德是伟大的古希腊数学家，他和高斯、牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），球的体积是圆柱体积的三分之二，球的表面积也是圆柱表面积的三分之二.今有一“圆柱容球”模型，其圆柱表面积为 $36 π$ ，则该模型中圆柱的体积与球的体积之和为（）

A、 $8 \sqrt{6} π$ B、 $12 \sqrt{6} π$ C、 $20 \sqrt{6} π$ D、 $48 \sqrt{6} π$

查看试题解析
6. 已知正四面体 $A B C D$ 的表面积为 $2 \sqrt{3}$ ，且 $A$ 、 $B$ 、 $C$ ， $D$ 四点都在球 $O$ 的球面上，则球 $O$ 的体积为（）

A、 $\frac{\sqrt{3}}{2} π$ B、 $\frac{\sqrt{3}}{4} π$ C、 $2 \sqrt{3} π$ D、 $3 π$

查看试题解析
7. 已知长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面 $A B C D$ 是边长为2的正方形， $A A_{1} = 4$ ， $M$ ， $N$ 分别为 $A A_{1}$ ， $C C_{1}$ 的中点，则三棱锥 $M - N B_{1} D_{1}$ 的体积为（）

A、 $\frac{4}{3}$ B、4 C、 $\frac{8}{3}$ D、6

查看试题解析
8. 已知母线长为a的圆锥的侧面展开图为半圆，在该圆锥内放置一个圆柱，则当圆柱的侧面积最大时，圆柱的体积为（）

A、 $\frac{\sqrt{3}}{128} π a^{3}$ B、 $\frac{\sqrt{3}}{64} π a^{3}$ C、 $\frac{\sqrt{3}}{32} π a^{3}$ D、 $\frac{\sqrt{3}}{16} π a^{3}$

查看试题解析
9. 如图，已知一个直四棱柱的侧棱长为 $6$ ，底面是对角线长分别是 $9$ 和 $13$ 的菱形，则这个四棱柱的侧面积是（）

A、 $30 \sqrt{10}$ B、 $40 \sqrt{10}$ C、 $50 \sqrt{10}$ D、 $60 \sqrt{10}$

查看试题解析

二、多项选择题

10. 已知圆台的上底半径为1，下底半径为3，球O与圆台的两个底面和侧面都相切，则（）

A、圆台的母线长为4 B、圆台的高为4 C、圆台的表面积为 $26 π$ D、球O的体积为 $12 π$

查看试题解析
11. 已知圆锥的底面半径为2，其侧面展开图为一个半圆，则下列说法正确的是（）

A、圆锥的高是 $\sqrt{2}$ B、圆锥的母线长是4 C、圆锥的表面积是 $16 π$ D、圆锥的体积是 $\frac{8 \sqrt{3}}{3} π$

查看试题解析
12. 已知圆柱的轴截面的周长为12，圆柱的体积为 $V$ ，圆柱的外接球的表面积为 $S$ ，则下列结论正确的是（）

A、圆柱的外接球的表面积 $S$ 有最大值，最大值为 $36 π$ B、圆柱的外接球的表面积 $S$ 有最小值，最小值为 $18 π$ C、圆柱的体积 $V$ 有最大值，最大值为 $8 π$ D、圆柱的体积 $V$ 有最小值，最小值为 $4 π$

查看试题解析
13. 在正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A_{1} B_{1} = 2 A B = 4$ ， $A A_{1} = 2$ ，则（）

A、该棱台的高为 $\sqrt{2}$ B、该棱台的表面积为 $20 + 12 \sqrt{3}$ C、该棱台的体积为 $28 \sqrt{2}$ D、该棱台外接球的表面积为 $40 π$

查看试题解析
14. 用平行于棱锥底面的平面去截棱锥，得到上､下两部分空间图形且上､下两部分的高之比为 $1 ： 2$ ，则关于上､下两部分空间图形的说法正确的是（）.

A、侧面积之比为 $1 ： 2$ B、侧面积之比为 $1 ： 8$ C、体积之比为 $1 ： 27$ D、体积之比为 $1 ： 26$

查看试题解析
15. 某班级到一工厂参加社会实践劳动，加工出如图所示的圆台 $O_{1} O_{2}$ ，在轴截面ABCD中， $A B = A D = B C = 2 c m$ ，且 $C D = 2 A B$ ，下列说法正确的有（）

A、 $∠ A D C = 30 °$ B、该圆台轴截面ABCD面积为 $3 \sqrt{3} c m^{2}$ C、该圆台的体积为 $\frac{7 \sqrt{3} π}{3} c m^{3}$ D、沿着该圆台表面，从点C到AD中点的最短距离为5cm

查看试题解析
16. 已知某圆锥的母线长为3，其侧面展开图是面积为 $3 π$ 的扇形，则（）

A、该扇形的弧长为 $π$ B、该扇形的圆心角为 $\frac{2 π}{3}$ C、该圆锥的底面半径为1 D、该圆锥的体积为 $\frac{2 \sqrt{2} π}{3}$

查看试题解析
17. 圆柱的侧面展开图是长6cm，宽4cm的矩形，则这个圆柱的体积可能是（）

A、 $\frac{24}{π} c m^{3}$ B、 $24 π c m^{3}$ C、 $\frac{36}{π} c m^{3}$ D、 $36 π c m^{3}$

查看试题解析
18. 一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径 $2 R$ 相等，下列结论正确的是（）

A、圆柱的侧面积为 $4 π R^{2}$ B、圆锥的侧面积为 $2 π R^{2}$ C、圆柱的侧面积与球的表面积相等 D、球的体积是圆锥体积的两倍

查看试题解析

三、填空题

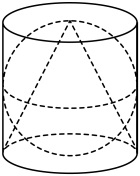
19. 已知圆锥底面半径为2，母线长为3，则圆锥的表面积为.

查看试题解析
20. 已知正四棱锥 $S - A B C D$ ，底面边长为2，体积为 $\frac{4 \sqrt{3}}{3}$ ，则这个四棱锥的侧棱长为.

查看试题解析
21. 把长和宽分别为6和3的矩形卷成一个圆柱的侧面，则该圆柱的体积为.

查看试题解析
22. 侧面均为面积为4的正方形的正三棱柱的表面积为．

查看试题解析
23. 一个圆锥的侧面展开图是一个扇形，已知扇形的半径为3，圆心角为 $\frac{2 π}{3}$ ，则扇形的弧长等于；该圆锥的体积等于.

查看试题解析
24. 已知圆锥表面积为 $6 π c m^{2}$ ，且它的侧面展开图是一个半圆，则这个圆锥底面半径是 $c m$ .

查看试题解析
25. 一个圆锥母线长为 $\sqrt{6}$ ，侧面积 $3 \sqrt{2} π$ ，则这个圆锥的外接球体积为．

查看试题解析
26. 如图所示的图案，是由圆柱、球和圆锥组成，已知球的直径与圆柱底面的直径和圆柱的高相等，圆锥的顶点为圆柱上底面的圆心，圆锥的底面是圆柱的下底面，则图案中圆锥、球、圆柱的体积 $V_{圆锥} ： V_{球} ： V_{圆柱} =$ .

查看试题解析

四、解答题

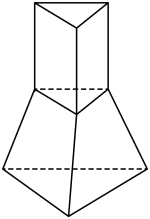
27. 如图，某铁质零件由一个正三棱台和一个正三棱柱组成，已知正三棱柱的底面边长与高均为1cm，正三棱台的下底面边长为2cm，且正三棱台的高为1cm，现有一盒这种零件共重 $650 \sqrt{3} g$ （不包含盒子的质量），取铁的密度为 $7.8 g / c m^{3}$ ．

(1)、试问该盒中有多少个这样的零件？

(2)、如果要给这盒零件的每个零件表面涂上一种特殊的材料，试问共需涂多少 $c m^{2}$ 的材料？

查看试题解析
28. 正六棱台玻璃容器的两底面棱长分别为 $7 c m$ ， $31 c m$ ，高为 $32 c m$ ，如图水平放置，盛有水深为 $12 c m$ ．

(1)、求玻璃容器的体积；

(2)、将一根长度为 $40 c m$ 的搅棒 $l$ 置入玻璃容器中， $l$ 的一端置于点 $E$ 处，另一端置于侧棱 $G G_{1}$ 上，求 $l$ 没入水中部分的长度． $($ 容器厚度，搅棒粗细均忽略不计 $)$

查看试题解析
29. 据《黑鞑事略》记载：“穹庐有二样：燕京之制，用柳木为骨，正如南方罘思，可以卷舒，面前开门，上如伞骨，顶开一窍，谓之天窗，皆以毡为衣，马上可载.草地之制，以柳木组定成硬圈，径用毡挞定，不可卷舒，车上载行.”随着畜牧业经济的发展和牧民生活的改善，穹庐或毡帐逐渐被蒙古包代替.如图1，一个普通的蒙古包可视为一个圆锥与一个圆柱的组合体.如图2，已知该圆锥的高为3米，圆柱的高为4米，底面直径为8米.求该蒙古包的侧面积.

查看试题解析
30. 如图所示，以线段AB为直径的半圆上有一点C，满足： $B C = 1$ ， $A C = \sqrt{3}$ ，若将图中阴影部分绕直线AB旋转180°得到一个几何体．

(1)、求阴影部分形成的几何体的体积；

(2)、求阴影部分形成的几何体的表面积．

查看试题解析

2023-2024学年高中数学人教A版必修二 8.3 简单几何体的表面积和体积 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修二 8.3 简单几何体的表面积和体积同步练习