2023-2024学年浙教版数学八年级(上)期末仿真模拟卷(杭州适用2)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列交通标志的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列语句中,不是命题的是( )A、两点之间线段最短. B、不平行的两条直线只有一个交点. C、x与y的差等于x-y吗? D、相等的角是对顶角.3. 已知图中的两个三角形全等,则∠1等于( )
2. 下列语句中,不是命题的是( )A、两点之间线段最短. B、不平行的两条直线只有一个交点. C、x与y的差等于x-y吗? D、相等的角是对顶角.3. 已知图中的两个三角形全等,则∠1等于( )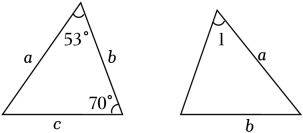 A、57° B、53° C、60° D、70°4. 在△ABC中,若∠A=∠B=∠C,则△ABC是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形5. 式子:①3<5;②4x+5>0;③x=3;④x2+x;⑤x≠4;⑥x+2≥x+1.其中是不等式的有( )A、2个 B、3个 C、4个 D、5个6. 一元一次不等式组的解在数轴上表示正确的是( )A、
A、57° B、53° C、60° D、70°4. 在△ABC中,若∠A=∠B=∠C,则△ABC是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形5. 式子:①3<5;②4x+5>0;③x=3;④x2+x;⑤x≠4;⑥x+2≥x+1.其中是不等式的有( )A、2个 B、3个 C、4个 D、5个6. 一元一次不等式组的解在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 平面直角坐标系中,点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 把点A(-2,1)向下平移2个单位后得到点B , 则点B的坐标是( )A、(-2,3) B、(-2,-1) C、(0,1) D、(-4,1)9. 下列函数中,是一次函数的是( )A、 B、 C、 D、10. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
7. 平面直角坐标系中,点所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 把点A(-2,1)向下平移2个单位后得到点B , 则点B的坐标是( )A、(-2,3) B、(-2,-1) C、(0,1) D、(-4,1)9. 下列函数中,是一次函数的是( )A、 B、 C、 D、10. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( ) A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为
A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为二、填空题(每题4分,共24分)
-
11. 不等式2x-3<1的正整数解是 .12. 如图,在△ABC中,AM是中线,AN是高。如果BM=3.5cm,AN=4 cm,那么△ABC的面积是cm2
 13. 已知点A(a , -2)与点B(-3,b)关于x轴对称 ,则a+b的值为 .14. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.
13. 已知点A(a , -2)与点B(-3,b)关于x轴对称 ,则a+b的值为 .14. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.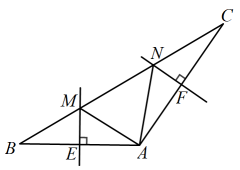 15. 购买某种瓜子应付金额如下表.
15. 购买某种瓜子应付金额如下表.质量x(千克)
1
2
3
……
应付金额y(元)
3.60+0.20
7.20+0.20
10.80+0.20
……
(1)、表中表示的是购买瓜子应付金额y与之间的函数关系.(2)、当x=4千克时,y=元16. 边长分别为4cm,3cm两正方体如图放置,点P在上,且 , 一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是cm.
三、解答题(共7题,共66分)
-
17. 补全横线上的内容并在括号中填入适当的理由:
如图, , , ;
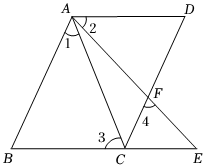
求证: .
证明:已知 ,
已知 ,
即 ▲ .
已知 ,
▲
18. 如图1,已知直线与相交于点O,平分 , 点G在射线上,点F在射线上,且 , 交于点P,若 , . (1)、求与的面积之比;(2)、比较与的大小并说明理由;(3)、如图2,当点M在线段上,点N在射线上,且 , 试问的值是否为定值;如果是,求出这个值;如果不是,请说明理由.19.(1)、分解因式: .(2)、解不等式组 , 并在数轴上表示出解集.20. 如图,在平面直角坐标内有三角形 , 其中 , , , 在坐标平面内放置一透明胶片,并在胶片上描画出点A.平移该胶片使点A落在点处.
(1)、求与的面积之比;(2)、比较与的大小并说明理由;(3)、如图2,当点M在线段上,点N在射线上,且 , 试问的值是否为定值;如果是,求出这个值;如果不是,请说明理由.19.(1)、分解因式: .(2)、解不等式组 , 并在数轴上表示出解集.20. 如图,在平面直角坐标内有三角形 , 其中 , , , 在坐标平面内放置一透明胶片,并在胶片上描画出点A.平移该胶片使点A落在点处. (1)、若点B,点C都与点A做同样的平移运动,点B,C平移后的对应点分别为点 , , 写出点 , 的坐标, ▲ , ▲ , 并在坐标平面内画出三角形 .(2)、求三角形的面积.21. 如图,将矩形置于平面直角坐标系中,其中边在x轴上且A的坐标是 , . 过点A的直线l交y轴于点 , 将直线l沿y轴的正方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形的边截得的线段长度为m , 平移时间为t秒,m与t的函数图象如图所示.
(1)、若点B,点C都与点A做同样的平移运动,点B,C平移后的对应点分别为点 , , 写出点 , 的坐标, ▲ , ▲ , 并在坐标平面内画出三角形 .(2)、求三角形的面积.21. 如图,将矩形置于平面直角坐标系中,其中边在x轴上且A的坐标是 , . 过点A的直线l交y轴于点 , 将直线l沿y轴的正方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形的边截得的线段长度为m , 平移时间为t秒,m与t的函数图象如图所示.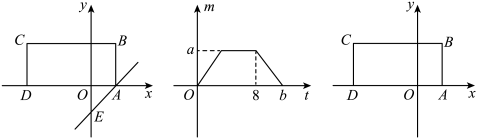 (1)、求直线l的函数解析式;(2)、直接写出矩形的面积,及图中a和b的值;(3)、在直线l的平移过程中,是否存在某个时刻使得直线l把矩形的面积分为的两部分,若成立,求出t的值;若不成立,请说明理由.22. 如图,在平面直角坐标系中,直线 与x轴,y轴分别交于A,B两点,点C(2,m)为直线 上一点,直线 过点C.
(1)、求直线l的函数解析式;(2)、直接写出矩形的面积,及图中a和b的值;(3)、在直线l的平移过程中,是否存在某个时刻使得直线l把矩形的面积分为的两部分,若成立,求出t的值;若不成立,请说明理由.22. 如图,在平面直角坐标系中,直线 与x轴,y轴分别交于A,B两点,点C(2,m)为直线 上一点,直线 过点C. (1)、求m和b的值;(2)、直线 与x轴交于点D,动点P在线段DA上从点D开始以每秒1个单位的速度向A点运动.设点P的运动时间为t秒.
(1)、求m和b的值;(2)、直线 与x轴交于点D,动点P在线段DA上从点D开始以每秒1个单位的速度向A点运动.设点P的运动时间为t秒.①若△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
23. 两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB=AC,AD=AE,∠BAC=∠DAE,连结BD,CE,则△ABD≌△ACE. (1)、请证明图1的结论成立;(2)、如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;(3)、如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
(1)、请证明图1的结论成立;(2)、如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,求∠BOC的度数;(3)、如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.