2023-2024学年广东省（人教版）九年级（上）数学期末模拟卷（二）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y＝﹣x²－3x＋1的图象的顶点在（）

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
3. 已知直角三角形的两条边长分别是方程x²﹣9x+20＝0的两个根，则此三角形的第三边是（）

A、4或5 B、3 C、 $\sqrt{41}$ D、3或 $\sqrt{41}$

查看试题解析
4. 一元二次方程x²﹣8x＋5＝0配方后可化为（）

A、（x﹣4）＝19 B、（x＋4）＝﹣19 C、（x﹣4）²＝11 D、（x＋4）²＝16

查看试题解析
5. 将抛物线y＝3x²的图象先向右平移2个单位，再向上平移5个单位后，得到的抛物线解析式是（）

A、y＝3（x﹣2）²﹣5 B、y＝3（x﹣2）²+5 C、y＝3（x+2）²﹣5 D、y＝3（x+2）²+5

查看试题解析
6. 若一元二次方程x²＋mx＋4＝0有两个相等的实数根，则m的值是（）

A、2 B、±2 C、±4 D、±2 $\sqrt{2}$

查看试题解析
7. 六张朴克牌中2张“方块”，3张“梅花”，1张“红桃”．将这六张牌背面朝上，从中任意抽取1张，是“红桃”的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
8. 如图，将△AOB绕点O按逆时针方向旋转60°后得到 $△ A O B$ ，若∠AOB＝25°，则 $∠ A O B^{^{'}}$ 的度数是（）

A、25° B、35° C、40° D、85°

查看试题解析
9. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的x与y的部分对应值如下表：
x
－2
－1
0
1
2
3
y
14
7
2
－1
－2
－1
则当 $x = 5$ 时，y的值为（）

A、－1 B、2 C、7 D、14

查看试题解析
10. 如图，若抛物线 $y = a x^{2} - 2 x + a^{2} - 1$ 经过原点，则抛物线的解析式为（）

A、 $y = - x^{2} - 2 x$ B、 $y = x^{2} - 2 x$ C、 $y = - x^{2} - 2 x + 1$ D、 $y = - x^{2} - 2 x$ 或 $y = x^{2} - 2 x$

查看试题解析

二、填空题（每题3分，共15分）

11. 已知点 $A (2 ， - 1)$ 与点 $A^{'}$ 关于原点对称，则点 $A^{'}$ 坐标为．

查看试题解析
12. 若2是关于 $x$ 的方程 $x^{2} - c = 0$ 的一个根，则 $c =$ ．

查看试题解析
13. 如图，在扇形 $A O B$ 中，半径 $O A$ 的长为2，点 $C$ 在弧 $A B$ 上，连接 $A C$ ， $B C$ ， $O C$ ，若四边形 $O B C A$ 为菱形，则图中阴影部分的面积为．（用含 $π$ 的代数式表示）

查看试题解析
14. 如图，CD是⊙O的直径，AB是弦，CD⊥AB于点E，若OA=5，AB=8，则AD的长为．

查看试题解析
15. 定义：关于x的方程 $a_{1} x^{2} + b_{1} x + c_{1} = 0$ （a₁≠0）与 $a_{2} x^{2} + b_{2} x + c_{2} = 0$ （a₂≠0），如果满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则称这两个方程互为“对称方程”．若关于x的方程 $3 x^{2} + (m^{2} - 2 m + 3) x - 4 = 0$ 与 $- 3 x^{2} + 2 x + n = 0$ 互为“对称方程”，则 $(m - n)^{2}$ 的值为．

查看试题解析

三、解答题（共8题，共75分）

16. 用适当的方法解下列方程：

(1)、 $x (x - 2) = x$ ；

(2)、 $x^{2} + 2 x - 3 = 0$

查看试题解析
17. 已知 $x = - 1$ 是关于 $x$ 的方程 $x^{2} + 2 a x + a^{2} = 0$ 的一个根，求 $a$ 的值．

查看试题解析
18. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣5，1），B（﹣2，2），C（﹣1，4），请按下列要求画图：

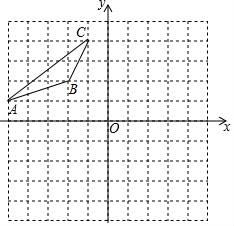(1)、将△ABC先向右平移4个单位长度、再向下平移1个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

(2)、画出与△ABC关于原点O成中心对称的△A₂B₂C₂ ，并直接写出点A₂的坐标．

查看试题解析
19. 已知：⊙O为Rt△ABC的外接圆，点D在边AC上，AD=AO；

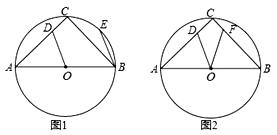(1)、如图1，若弦BE∥OD，求证：OD=BE；

(2)、如图2，点F在边BC上，BF=BO，若OD=2 $\sqrt{2}$ ， OF=3，求⊙O的直径．

查看试题解析
20. 苏宁电器销售某种冰箱，每台的进货价为2600元，调查发现，当销售价为3000元时，平均每天能售出8台；而当销售价每降低100元时，平均每天就能多售出8台. 商场要使这种冰箱的销售利润平均每天达到5000元，每台冰箱的定价应为多少元?

查看试题解析
21. 福田区某轿车销售公司为龙泉工业区代销 A 款轿车，为了吸引购车族，销售公司打出降价牌，今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元，如果卖出相同数量的 A 款轿车，去年的销售额为100万元，今年销售额只有90万元．

(1)、今年 5月份 A 款轿车每辆售价为多少元？

(2)、为了增加收入，该轿车公司决定再为龙泉工业区代销 B款轿车，已知 A款轿车每辆进价为 7.5万元，B款轿车每辆进价为 6万元，公司预计用不多于105万元的资金购进这两款轿车共 15 辆，但A款轿车不多于6辆，试问共有几种进货方案？

(3)、在⑵的条件下，B款轿车每辆售价为 8万元，为打开B款轿车的销路，公司决定每售出一辆 B款轿车，返还顾客现金a（ 0＜a ≤1 ）万元．假设购进的15辆车能够全部卖出去，试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润？

查看试题解析
22. 某校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，墙的最大可用长度为12米．另三边用总长为26米的木板材料围成．车棚形状如图1中的矩形 $A B C D$ ．为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门．

(1)、求这个车棚的最大面积是多少平方米？此时 $A B$ 与 $A D$ 的长分别为多少米？

(2)、如图2，在（1）的结论下，为了方便学生取车，施工单位决定在车棚内纵向、横向各修建2条、1条等宽的小路，使得停放自行车的面积为70平方米，那么小路的宽度是多少米

查看试题解析
23. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (5 ， 0)$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上存在一点 $P$ ，使得 $P A + P C$ 的值最小，求此时点 $P$ 的坐标；

(3)、点 $D$ 是第一象限内抛物线上的一个动点（不与点 $C$ 、 $B$ 重合），过点 $D$ 作 $D F ⊥ x$ 轴于点 $F$ ，交直线 $B C$ 于点 $E$ ，连接 $B D$ ，直线 $B C$ 把 $Δ B D F$ 的面积分成两部分，若 $S_{Δ B D E} ： S_{Δ B E F} = 3 ： 2$ ，请求出点 $D$ 的坐标．

查看试题解析

x	－2	－1	0	1	2	3
y	14	7	2	－1	－2	－1