2023-2024学年浙教版数学八年级（上）期末仿真模拟卷（杭州适用1）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题

1. 如图，点 $O$ 是 $△ A B C$ 内一点， $∠ A = 80 °$ ， $∠ 1 = 15 °$ ， $∠ 2 = 40 °$ ，则 $∠ B O C =$ （）

A、 $95 °$ B、 $120 °$ C、 $130 °$ D、 $135 °$

查看试题解析
2. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（）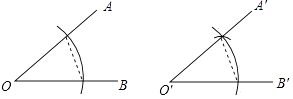

A、SAS B、ASA C、AAS D、SSS

查看试题解析
3. 已知一个等腰三角形的两边长分别是4，5，则它的周长是（）

A、13 B、14 C、9或12 D、13或14

查看试题解析
4. 如图所示.在△ABC中，∠C=90°，DE垂直平分AB，交BC于点E，垂足为点D，BE=6cm，∠B=15°，则AC等于（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
5. 若 $a > b$ ，则下列式子中正确的是（）

A、 $\frac{a}{2} < \frac{b}{2}$ B、 $a - 3 < b - 3$ C、 $- 3 a < - 3 b$ D、 $a - b < 0$

查看试题解析
6. 若不等式组 ${\begin{array}{l} x > 8 \\ x < 4 m \end{array}$ 无解，则 $m$ 的取值范围为（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析
7. 如图，是A，B，C，D四位同学的家所在位置，若以A同学家的位置为坐标原点建立平面直角坐标系，那么C同学家的位置的坐标为(1，5)，则B，D两同学家的坐标分别为（）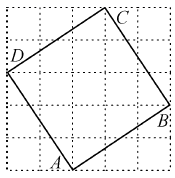

A、(2，3)，(3，2) B、(3，2)，(2，3) C、(2，3)，(-3，2) D、(3，2)，(-2，3)

查看试题解析
8. 在平面直角坐标系中，点A的坐标为 $(- 2 ， 10)$ ，点B与点A关于x轴对称，则点B的坐标为（）

A、 $(2 ， 10)$ B、 $(10 ， 2)$ C、 $(- 2 ， - 10)$ D、 $(10 ， - 2)$

查看试题解析
9. 已知点 $P (1 ， 4)$ 在直线 $y = k x - 2 k$ 上，则 $k$ 的值为（）

A、 $\frac{4}{3}$ B、 $- \frac{4}{3}$ C、4 D、-4

查看试题解析
10. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴交于点B，与y轴交于点C，点 $E (1 ， 0)$ ， D为线段 $B C$ 的中点，P为y轴上的一个动点，连接 $P D$ 、 $P E$ ，当 $△ P E D$ 的周长最小时，点P的坐标为（）

A、 $(0 ， \frac{4}{5})$ B、 $(0 ， 1)$ C、 $(1 ， 0)$ D、 $(0 ， \frac{3}{2})$

查看试题解析

二、填空题

11. 如图，若△ABC≌△DEF ， AF＝2，FD＝8，则FC的长度是．

查看试题解析
12. 如图，在△ABC中，∠C=30°，∠B=50°，AD平分∠CAB，那么∠ADC的度数是

查看试题解析
13. 命题：直角三角形两条直角边的平方和等于斜边的平方，其逆命题是.

查看试题解析
14. 不等式 $3 x + 4 \leq 10$ 的解集是.

查看试题解析
15. 若点 $A (2 ， a)$ 与点 $B (- 2 ， 5)$ 关于y轴对称，则a的值为 .

查看试题解析
16. 如图，在平面直角坐标系中，一次函数y=－2x+4的图象与x轴、y轴分别交于点A和点B ，过点B的直线BC：y=kx+b交x轴于点C（－8，0）.

(1)、k的值为；

(2)、点M为直线BC上一点，若∠MAB=∠ABO ，则点M的坐标是.

查看试题解析

三、解答题

17. 已知：如图，点 $A ， D ， B ， E$ 在同一条直线上， $A C = E F ， A D = B E ， B C = D F$ .求证： $∠ E D F = ∠ A B C$ .

查看试题解析
18. 如图，已知 $△ A B C$ 中， $A B = A C$ ，点D、E在直线BC上， $B D = C E$ ．

(1)、如图1，求证： $∠ D = ∠ E$ ；

(2)、如图2，过点D向下作 $D F ⊥ D C$ ，交AB的延长线于点F，若 $∠ D A E = 4 ∠ E$ ， $A B = F B$ ，求证： $A E = 2 D F$ ；

(3)、如图3，在（2）的条件下，延长FD、EA交于点G，连接BG，若 $S_{△ A B D} = \sqrt{3}$ ，求四边形ACBG的面积．

查看试题解析
19. 某蔬菜店第一次用 $800$ 元购进某种蔬菜，由于销售状况良好，该店又用 $1400$ 元第二次购进该品种蔬菜，所购数量是第一次购进数量的 $2$ 倍，但进货价每千克少了 $0.5$ 元．

(1)、第一次所购该蔬菜的进货价是每千克多少元？

(2)、蔬菜店在销售中，如果两次售价均相同，第一次购进的蔬菜有 $3 %$ 的损耗，第二次购进的蔬菜有 $5 %$ 的损耗，若该蔬菜店售完这些蔬菜获利不低于 $1244$ 元，则该蔬菜每千克售价是多少元？

查看试题解析
20. 如图

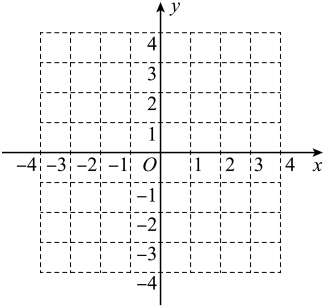(1)、在平面直角坐标系中，画 $△ A B C$ ，使其三个顶点为 $A (- 1 ， 0)$ ， $B (1 ， - 1)$ ， $C (3 ， 3)$ ；

(2)、 $△ A B C$ 是直角三角形吗？请证明你的判断.

查看试题解析
21. 如图1，平面直角坐标系中，直线y=kx+b与x轴交于点A（6，0），与y轴交于点B ，与直线y=2x交于点C（a ， 4）．

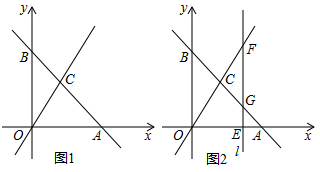(1)、求点C的坐标及直线AB的表达式；

(2)、如图2，在x轴上有一点E ，过点E作直线 $l$ ⊥x轴，交直线y=2x于点F ，交直线y=kx+b于点G ，若GF的长为3．求点E的坐标；

(3)、在y轴上是否存在一点F ，使以O、C、F为顶点的三角形是等腰三角形，若存在，直接写出点F的坐标；若不存在，说明理由．

查看试题解析
22. 为提升学生的文学素养，培养学生的阅读兴趣，某校准备购进A，B两种图书.经调查，购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示，B种图书每本20元.

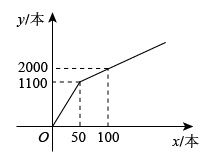(1)、当 $0 \leq x \leq 50$ 和 $x > 50$ 时，求y与x之间的函数关系式；

(2)、现学校准备购进300本图书，其中购进A种图书x本，设购进两种图书的总费用为w元.
①当 $x > 50$ 时，求出w与x间的函数表达式；
②若购进A种图书不少于60本，且不超过B种图书本数的2倍，那么应该怎样分配购买A，B两种图书才能使总费用最少？最少总费用多少元？

查看试题解析
23. 如图，已知点D是等边三角形 $A B C$ 中 $B C$ 边所在直线上的点，连接 $A D$ ，过点D作 $∠ A D F = 60 °$ ， $D F$ 与 $∠ A C B$ 的邻补角的平分线交于点F.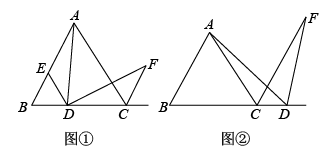

(1)、如图①，当点D在线段 $B C$ 上时，过点D作 $D E ∥ A C$ ，且交 $A B$ 于点E.求证： $B D = B E$ ；

(2)、如图①，在（1）的条件下，求证： $B C = C D + C F$ ；

(3)、如图②，当点D在线段 $B C$ 的延长线上时，（2）中线段 $B C$ ， $C D$ ， $C F$ 之间的数量关系式还成立吗？若成立，请加以证明；若不成立，请写出线段 $B C$ ， $C D$ ， $C F$ 之间新的数量关系式，并说明理由.

查看试题解析