2023-2024学年广东省（人教版）九年级（上）数学期末模拟卷（一）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = {(x - 3)}^{2} + 4$ 的顶点坐标是（）

A、 $(3 ， - 4)$ B、 $(- 3 ， 4)$ C、 $(- 3 ， - 4)$ D、 $(3 ， 4)$

查看试题解析
3. 已知关于 $x$ 的一元二次方程 $x^{2} + 3 x - 2 = 0$ ，下列说法正确的是（）

A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、方程没有实数根 D、方程的根为 $x_{1} = 1$ ， $x_{2} = - 2$

查看试题解析
4. 受国际油价影响，今年我国汽油价格总体呈上升趋势.已知某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 {(1 + x)}^{2} = 8.9$ B、 $8.9 {(1 + x)}^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 {(1 + x)}^{2} = 8.9$

查看试题解析
5. 关于 $x$ 的一元二次方程 $(k - 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $k$ 取值范围是（）

A、 $k \geq - 2$ B、 $k > 2$ C、 $k < 2$ 且 $k \neq 1$ D、 $k > 2$ 且 $k \neq 1$

查看试题解析
6. 圆心为O的两个同心圆，半径分别是2和3，若 $O P = \sqrt{8}$ ，则点P在（）

A、大圆上 B、小圆内 C、大圆外 D、大圆内、小圆外

查看试题解析
7. “小明经过有交通信号灯的路口，遇到绿灯”，这个事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、确定事件

查看试题解析
8. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（）
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333

A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 B、抛一个质地均匀的正六面体骰子，向上的面点数是5 C、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” D、抛一枚硬币，出现反面的概率

查看试题解析
9. 如图，在 $⊙ O$ 中， $O A = 2$ ， $∠ A C B = 45 °$ ，则图中阴影部分的面积为（）

A、 $π$ B、 $2 π$ C、 $\frac{π}{4}$ D、 $\frac{π}{2}$

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于点 $A (- 1 ， 0)$ ，顶点坐标为 $(1 ， n)$ ，与y轴的交点为B．有下列结论：① $2 a + b = 0$ ；② $9 a + 3 b + c = 0$ ；③若 $2 \leq c \leq 3$ ，则 $- 1 \leq a \leq - \frac{2}{3}$ ；④关于x的方程 $a x^{2} + b x + c - n + 1 = 0$ 有两个不相等的实数根．其中正确结论的个数是（）．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每题3分，共15分）

11. 若关于 $x$ 的方程 $x^{2} - k x - 12 = 0$ 的一个根为2，则 $k$ 的值为．

查看试题解析

12. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下表

种子粒数	100	400	800	1000	2000	5000
发芽种子粒数	85	298	652	793	1604	4005
发芽频率	0.850	0.745	0.815	0.793	0.802	0.801

根据以上数据可以估计，该玉米种子发芽的概率约为（精确到0.1）.

查看试题解析

13. 抛物线 $y = 2 {(x - 3)}^{2} + 4$ 的对称轴是直线．

查看试题解析
14. 如果点 $M (- 2 ， y_{1})$ ， $N (- 1 ， y_{2})$ 在二次函数 $y = - x^{2} + 2 x$ 的图象上，则 $y_{1}$ $y_{2}$ （填“＞”、“＜”或“＝”）

查看试题解析
15. 如图，在直角三角形 $A B C$ 中， $∠ A B C = 60 °$ ， $B C = \sqrt{3}$ ，将 $△ A B C$ 顺时针旋转 $15 °$ 得到 $△ A^{'} B C^{'}$ ， $A B$ 与 $A^{'} C^{'}$ 相交于点 $E$ ，则 $A^{'} E$ 的长为．（结果保留根号）

查看试题解析

三、解答题（共8题，共75分）

16.

(1)、解方程： $x^{2} - 6 x + 9 = (2 x - 1)^{2}$ ，

(2)、计算： $2^{- 1} + \sqrt{12} - 3 t a n 60 °$

查看试题解析
17. 用配方法解方程： $2 x^{2} - 4 x - 16 = 0$

查看试题解析
18. 用公式法解方程：2x²-4x-1=0

查看试题解析
19. 如图，在平面直角坐标系中， $Δ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$ ．

⑴请画出 $Δ A B C$ 关于原点对称的 $Δ A_{1} B_{1} C_{1}$ ；

⑵请画出 $Δ A B C$ 绕点 $B$ 逆时针旋转90°后的 $Δ A_{2} B_{2} C_{2}$ ，求点 $A$ 到 $A_{2}$ 所经过的路径长．

查看试题解析
20. 为落实我市关于开展中小学课后服务工作的要求，某学校开设了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．某年级共有100名学生选择了A课程，为了解本年级选择A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制）分成六组，绘制成频数分布直方图．

(1)、该年级学生小乔随机选取了一门课程，则小乔选中课程C的概率是；

(2)、根据题中信息，估计该年级选择A课程学生成绩在80≤x＜90的总人数；

(3)、该年级每名学生选两门不同的课程，小张和小王在选课程的过程中，若第一次都选了课程C，那么他俩第二次同时选择课程A或课程B的概率是多少？请用列表法或树状图的方法加以说明．

查看试题解析
21. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ 是劣弧 $B D$ 中点， $A C$ 与 $B D$ 相交于点 $E$ ．连接 $B C ， ∠ B C F = ∠ B A C ，$ $C F$ 与 $A B$ 的延长线相交于点 $F$ ．

(1)、求证： $C F$ 是 $⊙ O$ 的切线；

(2)、求证： $∠ A C D = ∠ F$ ；

(3)、若 $A B = 10 ， B C = 6$ ，求 $A D$ 的长．

查看试题解析
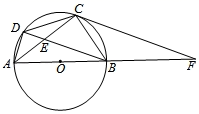22. 某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数的关系，其部分对应数据如下表所示：
每千克售价x（元）
…
25
30
35
…
日销售量y（千克）
…
110
100
90
…

(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？

查看试题解析
23. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求该抛物线的解析式及顶点坐标；

(2)、若点 $E$ 是抛物线的对称轴与直线 $B C$ 的交点，点 $F$ 是抛物线的顶点，求 $E F$ 的长；

(3)、抛物线上是否存在点 $P$ 使得 $S_{△ P A B} = 6$ ?如果存在，请求出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

每千克售价x（元）	…	25	30	35	…
日销售量y（千克）	…	110	100	90	…