2023-2024学年浙教版数学七年级（上）期末仿真模拟卷（杭州适用2）

试卷更新日期：2023-12-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 大于-1且小于2的整数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 已知a，b都是有理数，如果|a+b|=b-a，那么对于下列两种说法：①a可能是负数；②b一定不是负数．其中判断正确的是（）

A、①②都错 B、①②都对 C、①错②对 D、①对②错

查看试题解析
3. 下列各式计算结果为负数的是（）

A、(-4)+(-5) B、(-4)-(-5) C、(-4)×(-5) D、(-4)÷(-5)

查看试题解析
4. 一个三位数，百位数字比个位数字大3，且该数能被7整除，这个数可能是（）

A、316 B、427 C、714 D、916

查看试题解析
5. 下列各式计算正确的是（）

A、 $\sqrt{25}$ =±5 B、± $\sqrt{16}$ =4 C、 $\sqrt{(- 6)^{2}}$ =-6 D、 $\sqrt{9} -^{3} \sqrt{8}$ =1

查看试题解析
6. 按如图所示的运算程序，能使输出 $y$ 值为 $5$ 的是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 2$ ， $n = 0$ C、 $m = 2$ ， $n = 2$ D、 $m = 3$ ， $n = 2$

查看试题解析
7. 如果 $3 a^{m + 3} b^{4}$ 与 $a^{2} b^{n}$ 是同类项，则 $m n$ 的值为（）

A、4 B、-4 C、8 D、12

查看试题解析
8. 下列关于作图的语句中正确的是（）

A、画直线AB=10 cm B、画射线OB=10 cm C、已知A，B，C三点，过这三点画一条直线 D、过直线AB外一点画一条直线和直线AB垂直

查看试题解析
9. 下列说法中错误的是（）

A、两点之间线段最短 B、如果∠a=53°38'，那么∠a余角的度数为36°22' C、一个锐角的余角比这个角的补角小 D、互补的两个角一个是锐角一个是钝角

查看试题解析
10. 如图，数轴上的点O和点A分别表示0和10，点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（t不超过10秒）.若点P在运动过程中，当PB＝2时，则运动时间t的值为（）

A、 $\frac{3}{2}$ 秒或 $\frac{5}{2}$ 秒 B、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{15}{2}$ 秒 C、3秒或7秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒 D、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒

查看试题解析

二、填空题（每题4分，共24分）

11. 若火箭发射点火前5秒记作-5秒，则火箭发射点火后10秒应记作.

查看试题解析
12. 地球的平均半径约为6 371 000米．数据6 371 000可用科学记数法表示为

查看试题解析
13. 已知一个立方体的体积是 $27 c m^{3}$ ，那么这个立方体的棱长是 $c m$ .

查看试题解析
14. 《九章算术》是我国古代数学名著之一，卷七“盈不足”中有题译文如下：“今有人合伙买羊，每人出5钱，则差45钱；每人出7钱，则差3钱．问合伙人数、羊价各是多少？”则该题中合伙的人数为

查看试题解析
15. 若∠α=30.2°，则∠α的补角度数为(用“°、'”表示)．

查看试题解析
16. 有一个长方体水箱，从里面量得它的深度为 $30 c m$ ，底面长为 $25 c m$ ，宽为 $20 c m$ ，水箱里已盛有深度为 $a (c m) (a \leq 30)$ 的水.若往水箱里放入一个棱长为 $10 c m$ 的立方体铁块，则水箱的水深为 $c m$ .

查看试题解析

三、解答题（共7题，共66分）

17. 已知下列有理数，在数轴上表示下列各数，并按原数从小到大的顺序用“＜”把这些数连接起来．
-5，+3， $- | - 3.5 |$ ， 0， $- (- 2)$ ， -1

查看试题解析
18. 东方滴滴快车司机张师傅某天上午在东西走向的大街上连续接到六位客人（假设第一位客人下车后刚好第二位客人上车，以此类推），如果规定向东为正，向西为负，他这天上午行车里程（单位：千米）如下：-2，+10，-2，+8，-17，-3.

(1)、将最后一位乘客送到目的地时，张师傅距出发地多远？此时在出发地东边还是西边？

(2)、若汽车耗油量为0.1升/千米，这天上午张师傅共耗油多少升？

(3)、若滴滴快车的起步价为10元，起步里程为3千米（包括3千米），超过部分每米2元，请问张师傅这天上午收入多少元？

查看试题解析
19. 如果一个正方形ABCD的面积为69．

(1)、求正方形ABCD的边长a．

(2)、正方形ABCD的边长满足m<a<n，m，n表示两个连续正整数，求m，n的值．

(3)、m，n在满足(2)的条件下，求 $^{3} \sqrt{- m} - \sqrt{n}$ 的值．

查看试题解析
20. 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $x$ 台电子产品， $y$ 个配件 $(y > x > 0)$ .

(1)、分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）

(2)、若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？

查看试题解析
21. 某市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：
用水量/月
单价（元/ $m^{3}$ ）
不超过 $20 m^{3}$
$2.05$
超过 $20 m^{3}$ 的部分
$3.05$
另：每立方米用水加收 $0.8$ 元的城市污水处理费和 $0.15$ 元的城市附加费

(1)、根据上表，用水量每月不超过 $20 m^{3}$ ，实际每立方米收水费多少元？如果10月份某用户用水量为 $18 m^{3}$ ，那么该用户10月份应该缴纳水费多少元？

(2)、某用户11月份共缴纳水费80元，那么该用户11月份用水多少 $m^{3}$ ？

(3)、若该用户水表12月份出了故障，有25%的水量没有计入水表中，这样该用户在12月份只缴纳了54元水费，问该用户12月份实际应该缴纳水费多少元？

查看试题解析
22. 如图，P是线段AB上一点，AB＝18cm，C，D两动点分别从点P，B同时出发沿射线BA向左运动，到达点A处即停止运动.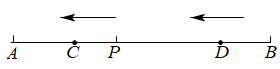

(1)、若点C，D的速度分别是1cm/s，2cm/s.
①当动点C，D运动了2s，且点D仍在线段PB上时，AC＋PD＝cm；
②若点C到达AP中点时，点D也刚好到达BP的中点，则AP∶PB＝；

(2)、若动点C，D的速度分别是1cm/s，3cm/s，点C，D在运动时，总有PD＝3AC，求AP的长度.

查看试题解析
23. 如图①， $∠ 1$ 、 $∠ 2$ 是四边形 $A B C D$ 的两个不相邻的外角．

(1)、猜想并说明 $∠ 1 + ∠ 2$ 与 $∠ A$ 、 $∠ C$ 的数量关系；

(2)、如图②，在四边形 $A B C D$ 中， $∠ A B C$ 与 $∠ A D C$ 的平分线交于点 $O$ ．若 $∠ A = 60 °$ ， $∠ C = 130 °$ ，求 $∠ B O D$ 的度数；

(3)、如图③， $B O$ 、 $D O$ 分别是四边形 $A B C D$ 外角 $∠ C B E$ 、 $∠ C D F$ 的角平分线．请直接写出 $∠ A$ 、 $∠ C$ 与 $∠ O$ 的数量关系．

查看试题解析

用水量/月	单价（元/ $m^{3}$ ）
不超过 $20 m^{3}$	$2.05$
超过 $20 m^{3}$ 的部分	$3.05$
另：每立方米用水加收 $0.8$ 元的城市污水处理费和 $0.15$ 元的城市附加费