2023-2024学年广东省(人教版)八年级(上)数学期末模拟卷(三)
试卷更新日期:2023-12-11 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 等腰三角形的两边分别为3和6,则这个三角形的周长是( )A、9 B、12 C、15 D、12或152. 在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A、40° B、45° C、50° D、60°3. 若 , , 则( )A、 B、 C、2 D、34. 安装空调一般会采用如图的方法固定,其根据的几何原理是( )
 A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短5. 下列计算正确的是( )A、 B、 C、 D、6. 要使得分式无意义,则的取值范围为( )A、 B、 C、 D、7. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )
A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短5. 下列计算正确的是( )A、 B、 C、 D、6. 要使得分式无意义,则的取值范围为( )A、 B、 C、 D、7. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )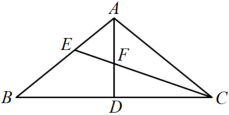 A、 B、 C、 D、8. 如图,平分 , 下列结论中,正确的个数是( )
A、 B、 C、 D、8. 如图,平分 , 下列结论中,正确的个数是( )
.
A、1 B、2 C、3 D、49. 对于两个不相等的实数a、b,我们规定符号Min{a,b}表示a、b中较小的值,如Min{2,4}=2,按照这个规定,方程Min{}=的解为( )A、1或3 B、1或-3 C、1 D、310. 如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想办法在作业本画了一样的三角形,那么这两个三角形完全一样的依据是( ) A、AAS B、ASA C、SSS D、SAS
A、AAS B、ASA C、SSS D、SAS二、填空题(每题3分,共15分)
-
11. 已知点M(﹣6,2),则M点关于x轴对称点的坐标是.12. 若 , , 则 .13. 使得分式有意义的条件是 .14. 如图,在等腰△ABC中,AB=AC=13,BC=10,D是BC边上的中点,M、N分别是AD和AB上的动点.则BM+MN的最小值是 .
 15. 如图:在平面直角坐标系中,已知正比例函数与一次函数的图象交于点A,设x轴上有一点P作x轴的垂线(垂足位于点A的右侧),分别交和的图象于点B、C,连接OC,若 , 则△OBC的面积为 .
15. 如图:在平面直角坐标系中,已知正比例函数与一次函数的图象交于点A,设x轴上有一点P作x轴的垂线(垂足位于点A的右侧),分别交和的图象于点B、C,连接OC,若 , 则△OBC的面积为 .
三、解答题(共8题,共75分)
-
16. 计算:(1)、;(2)、 .17. 先化简,再求值: , 其中x=-2.18. 如图,△ABC中,∠C=90°,∠A=30°.
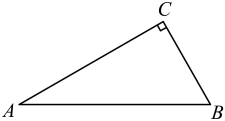 (1)、用尺规作图作∠CBA的角平分线BD,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)、在上图中,若BD=10cm,求DC的长19. 如图,P是内一点,于点A,于点B,连接 , . 求证:平分 .
(1)、用尺规作图作∠CBA的角平分线BD,交AC于点D(保留作图痕迹,不要求写作法和证明);(2)、在上图中,若BD=10cm,求DC的长19. 如图,P是内一点,于点A,于点B,连接 , . 求证:平分 .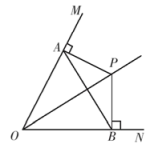 20. 水果店第一次用500元购进某种水果,由于销售状况良好,该店又用1650元购进该品种水果,所购数量是第一次购进数量的3倍,但进货价每千克多了0.5元.(1)、第一次所购水果的进货价是每千克多少元?(2)、水果店以每千克8元销售这些水果,在销售中,第一次购进的水果有5%的损耗,第二次购进的水果有2%的损耗.该水果店售完这些水果可获利多少元?21. 我们常采用构造几何图形的方法对代数式的变形加以说明.如图,利用图1中边长分别为 , 的正方形,以及长为、宽为的长方形卡片若干张,拼成图2正方形和图3长方形.
20. 水果店第一次用500元购进某种水果,由于销售状况良好,该店又用1650元购进该品种水果,所购数量是第一次购进数量的3倍,但进货价每千克多了0.5元.(1)、第一次所购水果的进货价是每千克多少元?(2)、水果店以每千克8元销售这些水果,在销售中,第一次购进的水果有5%的损耗,第二次购进的水果有2%的损耗.该水果店售完这些水果可获利多少元?21. 我们常采用构造几何图形的方法对代数式的变形加以说明.如图,利用图1中边长分别为 , 的正方形,以及长为、宽为的长方形卡片若干张,拼成图2正方形和图3长方形. (1)、请写出一个能够表示图2面积关系的乘法公式;(2)、请用两种不同的代数式表示图3的面积;(3)、根据(2)所得的结果,写出一个表示因式分解的等式.22. 阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为﹣(a+b),所以关于x的方程x+=a+b的解为x1=a,x2=b.(1)、理解应用:方程的解为:x1= , x2=;(2)、知识迁移:若关于x的方程x+=5的解为x1=a,x2=b,求a2+b2的值;(3)、拓展提升:若关于x的方程=k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+2t3的值.23. 阅读材料:如图1,已知Rt△ABC中,∠C=90°,请用尺规作图在AB边上求作点P,使得∠BPC+∠ACP=90°.
(1)、请写出一个能够表示图2面积关系的乘法公式;(2)、请用两种不同的代数式表示图3的面积;(3)、根据(2)所得的结果,写出一个表示因式分解的等式.22. 阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为﹣(a+b),所以关于x的方程x+=a+b的解为x1=a,x2=b.(1)、理解应用:方程的解为:x1= , x2=;(2)、知识迁移:若关于x的方程x+=5的解为x1=a,x2=b,求a2+b2的值;(3)、拓展提升:若关于x的方程=k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+2t3的值.23. 阅读材料:如图1,已知Rt△ABC中,∠C=90°,请用尺规作图在AB边上求作点P,使得∠BPC+∠ACP=90°.小明提出想法:如图2,假设点P为所求作的点,连接CP,此时有∠BPC+∠ACP=90°,因为∠BCP+∠ACP=90°,所以∠BPC=∠BCP,从而得到:BP=BC.
由此想法得到如下作图方法:如图2,以点B为圆心,BC为半径画弧,该弧与AB相交于点P,则点P即为所作的点.
根据以上材料,完成下面两个问题:
 (1)、请你类比上述作图方法,在图2中,用尺规作图在AB边上求作点Q,使得∠CQB+∠A=180°.(2)、在(1)的条件下,
(1)、请你类比上述作图方法,在图2中,用尺规作图在AB边上求作点Q,使得∠CQB+∠A=180°.(2)、在(1)的条件下,①若AC=6,AB=10,求PQ的长.
②请直接写出∠PCQ与∠B之间的数量关系是 .