2023-2024学年初中数学八年级上册 4.3 一元一次不等式的解法 同步分层训练培优卷(湘教版)
试卷更新日期:2023-12-11 类型:同步测试
一、选择题
-
1. 小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元,每支钢笔5元,小聪最多可以购买钢笔多少支?设小聪最多能买x支钢笔.可列出不等式( )A、 B、 C、 D、2. 某种毛巾原零售价为每条6元,凡一次性购买两条以上,商家推出两种优惠销售办法,第一种:“两条按原价,其余按七折付款”;第二种:“全部按原价的八折付款”.若想在购买相同数量的情况下,要使第一种办法比第二种办法得到的优惠多,最少要购买毛巾( )A、4条 B、5条 C、6条 D、7条3. 不等式的解是( )A、 B、 C、 D、4. 不等式的解为( )A、 B、 C、 D、5. 下列哪个数是不等式2(x-1)+3<0的一个解( )A、2 B、 C、- D、-36. 已知不等式的负整数解恰好是-3,-2,-1,那么满足条件( )A、 B、 C、 D、7. 下列命题中,是真命题的是( )A、全等三角形的对应角相等 B、面积相等的两个三角形是全等三角形 C、的解是 D、如果 , 则8. 定义新运算“⊕”如下:当a>b时,a⊕b=ab+b;当a<b时,a⊕b=ab-b,若3⊕(x+2)>0,则x的取值范围是( )A、-1<x<1或x<-2 B、x<-2或1<x<2 C、-2<x<1或x>1 D、x<-2或x>2
二、填空题
-
9. 根据数量关系:x的3倍加上1是正数,可列出不等式: .10. 用不等式表示:“x的3倍不大于5 ”是.11. 已知:不等式2x-m≤0只有三个正整数解,则化简 +|m-9|= .12. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1。如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解为。
13. 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动次后该点到原点的距离不小于41
三、解答题
-
14. 当 x取何正整数值时, 代数式 与 的值的差大于1.15. 若三角形的三边长分别是2、x、8,且x是不等式 >- 的正整数解,试求第三边x的长.
四、综合题
-
16. 已知关于 x,y 的二元一次方程组 的解满足.(1)、求 k 的取值范围;(2)、在 (1) 的条件下,若不等式的解为 , 请写出符合条件的 k 的整数值.17. 深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为 ,
即:当n为非负整数时,如果 ;
反之,当n为非负整数时,如果
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)、填空:① =(
=( 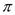 为圆周率); ②如果 的取值范围为.
(2)、若关于x的不等式组 的整数解恰有3个,求a的取值范围.(3)、求满足 的所有非负实数x的值.
为圆周率); ②如果 的取值范围为.
(2)、若关于x的不等式组 的整数解恰有3个,求a的取值范围.(3)、求满足 的所有非负实数x的值.